Вот некоторые основные понятия, относящиеся к расширениям модулей и групп.
1) Пусть

--- ассоциативное кольцо,

и
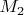
---

-модули.
Расширение 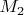 с помощью
с помощью 
--- это короткая точная последовательность

-модулей вида

Также расширением
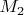
с помощью

называется средний модуль

, фигурирующий в этой последовательности. (А иногда говорят (в теории групп особенно) наоборот, что

--- расширение

с помощью
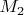
.)
Если имеется коммутативная диаграмма вида
![$$ \xymatrix{ 0\ar[r] & M_1\ar[r]^{\alpha_1}\ar@{=}[d] & M \ar[r]^{\beta_1}\ar[d]^{\varphi} & M_2\ar[r]\ar@{=}[d]
& 0 \\ 0\ar[r] & M_1\ar[r]^{\alpha_2} & M'\ar[r]^{\beta_2} & M_2\ar[r] & 0 } $$ $$ \xymatrix{ 0\ar[r] & M_1\ar[r]^{\alpha_1}\ar@{=}[d] & M \ar[r]^{\beta_1}\ar[d]^{\varphi} & M_2\ar[r]\ar@{=}[d]
& 0 \\ 0\ar[r] & M_1\ar[r]^{\alpha_2} & M'\ar[r]^{\beta_2} & M_2\ar[r] & 0 } $$](https://dxdy-02.korotkov.co.uk/f/5/7/8/578bbda222d77446d46f3700fc97db7a82.png)
то расширения, представленные строками этой диаграммы, называются конгруэнтными. Конгруэнтность расширений ---
отношение эквивалентности. См.
Маклейн, Гомология, гл.3.
Множество классов эквивалентности расширений
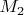
с помощью

обозначается

. На самом деле,

--- первый из серии так называемых "когомологических функторов"

, так что обычно пишется

, а не просто

.
На множестве

можно ввести некоторую операцию сложения, относительно которой оно является абелевой группой.
-- 20.07.2018, 01:39 --2) Теперь обратимся к расширениям групп. Пусть

и

--- две группы.
Расширение  с помощью
с помощью 
--- это короткая точная последовательность групп

(или просто группа

, фигурирующая в этой последовательности). Аналогично случаю модулей, два расширения считаются эквивалентными, если существует коммутативная диаграмма вида
![$$ \xymatrix{ 1\ar[r] & N\ar[r]^{\alpha_1}\ar@{=}[d] & G_1 \ar[r]^{\beta_1}\ar[d] & H\ar[r]\ar@{=}[d] & 1 \\
1\ar[r] & N\ar[r]^{\alpha_2} & G_2\ar[r]^{\beta_2} & H\ar[r] &1 } $$ $$ \xymatrix{ 1\ar[r] & N\ar[r]^{\alpha_1}\ar@{=}[d] & G_1 \ar[r]^{\beta_1}\ar[d] & H\ar[r]\ar@{=}[d] & 1 \\
1\ar[r] & N\ar[r]^{\alpha_2} & G_2\ar[r]^{\beta_2} & H\ar[r] &1 } $$](https://dxdy-03.korotkov.co.uk/f/a/f/6/af626971445191ffc929ba5bbd62535b82.png)
Обозначим множество классов эквивалентности расширений через

. (Выше
g______d обозначал это
множество через

. Но, кажется, по отношению к расширениям групп такое обозначение нигде не употребляется; главное же, что и само это множество не рассматривается, по причинам, которые будут объяснены чуть ниже. )
Множество

определяется "похоже" на то, как определяется

. Однако свойства
этого множества совершенно другие. Это не группа или что-то вроде, а просто множество. Поэтому изучать его "в целом"
было бы трудно. Его и не изучают. Ниже мы увидим, что изучать его в целом вообще нет необходимости. Тем не менее,
внутри него есть части, которые поддаются изучению.
-- 20.07.2018, 01:42 --3) Напомним кое-что о группах. Пусть

--- группа, и

. Отображение

--- автоморфизм группы

(называемый
внутренним автоморфизмом).

, так что

--- гомоморфизм из

в

. Ядро этого гомоморфизма есть

(центр

), а образ обозначают

. Если

,

можно отождествлять с

. Кроме того, всегда

(

--- знак нормальной подгруппы). Факторгруппа

называется группой внешних автоморфизмов группы

.
Более общо, пусть
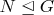
. Тогда

инвариантна относительно всех

. Поэтому имеется
гомоморфизм

. Ядро

есть
 централизатор
централизатор 
в

. В частности, если

, то

является подгруппой в

,
содержащей

.
Композиция

с эпиморфизмом

дает гомоморфизм

. Легко понять, что

, так что
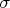
пропускается через
факторгруппу

, и получается гомоморфизм

. В частности, когда

абелева, имеем гомоморфизм

.
Теперь пусть

Отождествляя

с

посредством

, а

с

в силу

, видим, что последнее расширение индуцирует некоторый гомоморфизм

. Легко видеть, что
для двух эквивалентных расширений гомоморфизм
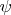
--- один и тот же т.е. определяется только классом
эквивалентности расширения.
Пусть

--- совокупность классов эквивалентности расширений, отвечающих данному

. Отметим, что

может быть пусто.
Тогда имеем разбиение

разбиение по всем

. Множества

--- это и есть
те "малые части"

, которые допускают изучение.
-- 20.07.2018, 01:45 --4) Пусть сначала

абелева. Будем писать

вместо

в этом случае. Заметим, что в силу того, что
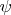
--- гомоморфизм из

в

,

является (левым)

-модулем.
Тогда

всегда непусто, так как содержит расширение

где

--- полупрямое произведение. Обычно считают
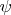
уже заданным раз и навсегда, и в обозначениях
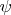
опускают, пишут просто

.
На

можно определить структуру абелевой группы, некоторым образом. Более того, эта группа изоморфна группе 2-когомологий

где

--- группа всех
2-коциклов, т.е. отображений

, удовлетворяющих
условию

а

--- группа
2-кограниц, т.е. отображений

, имеющих вид

для некоторого отображения

.
-- 20.07.2018, 01:48 --5) Теперь рассмотрим случай, когда

--- не обязательно абелева. Пусть

.
Отметим, что

действует тождественно на

, и поэтому

является

-модулем. Поэтому
можно рассматривать группу 3-когомологий

. Оказывается, что можно некоторым образом сопоставить
гомоморфизму
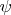
класс 3-когомологий

таким образом, что

непусто тогда и только тогда, когда

. Кроме того, если

, то множество

можно перенумеровать элементами группы

(более точно, существует некоторое каноническое регулярное действие группы

на

.)
6) На самом же деле оказывается, что в рассмотрении групп 3-когомологий особой надобности нет (в задаче о строении групп; в других задачах, возможно, и есть). Поясним причину этого.
Будем рассматривать группы

только конечные, или же бесконечные, но по крайней мере имеющие конечный
композиционный ряд. В любой такой группе

, очевидно, есть нетривиальная минимальная нормальная подгруппа

(т.е. не существует нормальных подгрупп

таких, что

). Пусть

обозначает подгруппу,
порожденную всеми минимальными нормальными подгруппами (т.наз.
цоколь группы

).
Утверждение. Либо  имеет нетривиальную абелеву нормальную подгруппу
имеет нетривиальную абелеву нормальную подгруппу  , либо
, либо  . В последнем случае
. В последнем случае  , где
, где  --- некоторые минимальные нормальные подгруппы в
--- некоторые минимальные нормальные подгруппы в  , и каждая
, и каждая  имеет вид
имеет вид  , где
, где  --- некоторая неабелева простая группа.
--- некоторая неабелева простая группа. (Доказательство этого утверждения следует из результатов главы 8 в кн.
М.Холл, Теория групп.)
Последнее утверждение может быть использовано для изучения строения групп следующим образом. Если в группе

есть абелева нормальная подгруппа

, то ее строение определяется некоторым когомологическим классом

(мы предполагаем, что у нас уже есть некоторые сведения о группе

и ее действии на

).
Если же абелевой нормальной подгруппы нет, то

, откуда

есть некоторая подгруппа в

, содержащая

в качестве нормальной подгруппы и, таким образом, восстанавливающаяся по группе

, которая является подгруппой в

(а последняя группа сравнительно несложно описывается).
-- 20.07.2018, 01:51 --7) Следует сделать еще одно замечание. Разные классы когомологий из

соответствуют, по определению,
неэквивалентным расширениям

Но при этом "средние" группы

могут оказаться изоморфными. Именно из-за этого феномена задача об описании всех непростых конечных групп фактически неразрешима.
Поясним последнее утверждение на пальцах. Опуская кое-какие мотивировки, опишем следующую конструкцию.
Пусть

--- нечетное простое число,

,

. Пусть

--- билинейное
отображение (мы можем говорить о билинейных отображениях, так как оба

и

можно рассматривать как пространства над полем из

элементов). Определим на множестве

умножение по правилу

Тогда можно проверить, что относительно этого умножения

--- группа. Обозначим ее

.
На пространстве всех отображений

указанного типа действует группа

. Можно
показать, что если отображения

и

лежат в одной орбите относительно данного действия, то

. Более того, если оба

и

кососимметричны,

и

(где

то условие
 эквивалентно
эквивалентно тому, что

и

лежат в одной орбите. Поэтому задача о классификации групп

указанного типа с точностью до изоморфизма эквивалентна задаче о классификации отображений

с точностью до действия группы

. А эта задача в случае, когда

, содержит в себе "задачу о паре матриц", и тем самым в определенном смысле неразрешима.
(Задача о паре матриц --- это задача о приведении пары матриц к каноническому виду одновременным преобразованием подобия:

Когда матрица одна, то ее можно привести к жордановой форме (над алгебраически замкнутым полем) или к канонической рациональной форме (над произвольным полем). Если же матриц две или больше, то разумного решения эта задача не допускает. Задача о паре матриц --- это эталонный пример "дикой" задачи, типа NP-полных задач
в теории сложности. Я с соответствующим концепциями едва знаком, поэтому точнее сказать не могу.)



