1) Как-то странно, что

может быть пусто. Я думал, по данному

всегда можно построить

Можно привести простенький пример?
Можно привести пример. Однако такой пример не может быть слишком простым. В частности, обязательно

.
Прежде всего, заметим следующее. Допустим, что подгруппа

дополняема в

, т.е.
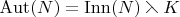
для некоторой подгруппы

. Это эквивалентно тому, что
отображение

имеет сечение, т.е. существует такой гомоморфизм

, что композиция

--- тождественное отображение на

. Тогда всегда

непусто. В самом деле, рассмотрим композицию

возьмем полупрямое произведение

, тогда достаточно рассмотреть точную последовательность

(стрелки определены очевидным образом).
(примечание)
Напомним, что полупрямое произведение

, где

--- какой-либо гомоморфизм из

в

, определяется следующим образом:

как множество, а умножение дается правилом

Для любой абелевой группы

имеем

. Также легко проверить, что для любой неабелевой группы порядка

подгруппа

дополняема в

. Значит,

может быть пусто, только если

--- неабелева группа порядка

.
Такой пример с

и

есть. Иначе говоря, существует группа

порядка 16, и внешний автоморфизм

порядка 2, для которых не существует группы

, содержащей

в качестве подгруппы
индекса 2, причем внешний автоморфизм группы

, индуцированный элементом

, совпадал бы с

.
Пусть

--- диэдральная группа порядка 16, т.е. группа симметрий правильного 8-угольника. Она может быть задана образующими и соотношениями как

Рассмотрим элементы

и

. Тогда

и

удовлетворяют определяющим соотношениям для

,

. Поэтому существует гомоморфизм

такой, что

,

. Кроме того,

, поэтому

сюръективен, следовательно, является автоморфизмом. Этот автоморфизм не является
внутренним, так как

и

не сопряжены в

.
В качестве

возьмем класс автоморфизма

в

. Покажем, что
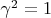
, т.е. что

--- внутренний автоморфизм. Имеем


Но сопряжение элементом

переводит

в себя, а

в

, т.е. совпадает с

. Значит,

--- внутренний, откуда
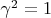
.
Теперь допустим, от противного, что группа

с искомыми свойствами существует. Пусть

. Сопряжение элементом

индуцирует автоморфизм

группы

, класс которого в

совпадает с

. Имеем

, где

. Пусть

--- элемент такой, что сопряжение элементом

действует на

как

. Тогда сопряжение элементом
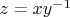
действует на

как

:

, для любого

. Поэтому сопряжение элементом

действует на

как

, т.е. так же, как сопряжение элементом

. Кроме того,

. Значит,

, где

--- элемент из центра группы

, т.е.
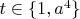
. Таким образом,

или

.
Очевидно,

должно коммутировать с

. Т.е.

должно быть инвариантным относительно

. Однако ни

, ни

--- не инвариантны (а именно,

переставляет их между собой). Противоречие.