Вопрос о классификации групп (и не только групп)

[Chanzaa]

xjar1 в сообщении #1317493 писал(а):

множество всех групп является множеством?

Не является. На любом непустом множестве можно задать структуру группы: для конечных множеств достаточно рассмотреть биекцию в группу вычетов по соответствующему модулю, на счетном множестве - в группу всех целых чисел по сложению, на несчётном мощности k - в сумму k экземпляров целых чисел (нужную биекцию обеспечит аксиома выбора). Все эти группы разные, так как у них различаются носители. То есть имеем инъекцию непустых множеств в группы. Чтобы достроить её до инъекции на всех множествах, нужно ещё сопоставить какую-нибудь отличную от использованных группу пустому множеству. Но понятно, что найдется хотя бы одно множество, на котором есть две разные структуры группы, так что пустое множество тоже можно куда-нибудь отправить. Таким образом, разных групп не меньше, чем разных множеств. А класс всех множеств уже не множество в ZFC.

[nya]

Вопросы мощности они не то чтобы совсем по существу, теорема о компактности говорит что любая бесконечная модель теории групп элементарно эквивалентна некоторой счетной модели, поэтому уже в счетных группах лежит вся сложность.

[xjar1]

Anton_Peplov в сообщении #1317487 писал(а):

Что Вы подразумеваете под "какой-то частью" бесконечного множества? Как Вы определите на нём половину, четверть, 99%?
Если что, последний вопрос - наводящий и адресован строго к ТС.

Сейчас задумался об этом, можно ли, например, сказать что чисел, делящихся на 2 больше, чем делящихся на 4? Мы ведь имеем $|2\mathbb{Z}|=|4\mathbb{Z}|$

[Anton_Peplov]

xjar1 в сообщении #1317632 писал(а):

Сейчас задумался об этом, можно ли, например, сказать что чисел, делящихся на 2 больше, чем делящихся на 4?

Можно, если понимать слово "больше" подходящим образом. Разумеется, его нельзя здесь понимать в смысле мощности множества, на что Вы сами и указали. Можно, например, ввести на $2\mathbb N$ меру $m$ так, чтобы выполнялось $m(4\mathbb N) = \frac 1 2 m(2\mathbb N)$. Это сделать легко, непонятно лишь, зачем это нужно, кроме как чтобы гордо чтобы гордо заявить, что чисел, делящихся на 4, "в некотором разумном смысле" (с) Chanzaa в два раза больше, чем делящихся на два. Какие математические задачи предполагается решить с помощью такой меры?

[Someone]

Да, подходящую меру на множестве $\mathbb N$ придумать нетрудно. Вообще, подобные меры встречаются в теории вероятностей. Но применяются ли они в теории чисел, не знаю. По-моему, там гораздо чаще встречаются всякие плотности.

Для множества $A\subseteq\mathbb{N}$ обозначим $k_A(n)$ количество элементов множества $A$, не превосходящих числа $n\in\mathbb{N}$ (считаем, что $0\notin\mathbb{N}$). Тогда можно рассмотреть, например, такие плотности:
$p(A)=\lim\limits_{n\to\infty}\frac{k_A(n)}n$ (асимптотическая плотность);

$d(A)=\inf\limits_{n\in\mathbb{N}}\frac{k_A(n)}n$ (плотность Шнирельмана).

Тогда $p(2\mathbb{N})=\frac 12$, $p(4\mathbb{N})=\frac 14$.

P.S. Плотность — ни в коем случае не вероятность и вообще не мера.

[xjar1]

Спасибо за пояснения!

Читал, что доказательство классификационной теоремы для простых конечных групп занимает 10–15 тысяч страниц. Как обычному человеку объять его? Или в доказательстве этой теоремы активно используется компьютер, и некоторая часть доказательства представляет собой код и результат его выполнения?

[Munin]

Обычному человеку и не нужно доказательство. Обычному человеку нужен результат.
https://ru.wikipedia.org/wiki/Классификация_простых_конечных_групп
https://en.wikipedia.org/wiki/Classification_of_finite_simple_groups

[xjar1]

Прошу прощения за поднятие темы, но возник еще один вопрос.

Цитата:

Из конечных простых групп можно построить любую конечную группу, так же, как любое натуральное число можно разложить в произведение простых.

Что под этим имеется ввиду? Как строится это разложение? Как прямая сумма, (полу)прямое произведение, или что-то другое?

[Munin]

Нужны и прямые произведения, и полупрямые. Но достаточно ли их - я не знаю, поскольку новичок. Послушаю знающих товарищей.

(В конечном случае прямая сумма и прямое произведение - вроде как одинаковые понятия.)

[nya]

Недостаточно, я же уже говорил в этой теме, что Z/4Z не получить таким образом.

-- 05.07.2018, 11:55 --

Munin в сообщении #1324517 писал(а):

(В конечном случае прямая сумма и прямое произведение - вроде как одинаковые понятия.)

В категории групп прямые суммы - это свободные произведения групп, а произведения это, собственно произведения.

-- 05.07.2018, 12:10 --

Любая группа имеет композиционный ряд - максимально возможную по длине возрастающую цепочку подгрупп каждый член которой нормален в следующей. Частичные факторы будут искомым "разложением на простые группы". Восстановить исходную группу по разложению можно операциями центрального расширения, чтобы постановление прошло однозначно на каждом шаге нужно зафиксировать по элементу а соответствующих когомологиях. Классифицировать все группы имеющие данное разложение это то что называется "программой гельдера" или "задачей расширения" (extension problem), насколько я знаю, большинство специалистов придерживаются ТЗ что эта задача крайне нереалистична и намного сложнее классификации простых конечных

-- 05.07.2018, 12:11 --

Chanzaa в сообщении #1317508 писал(а):

На любом непустом множестве можно задать структуру группы

Это, кстати, эквивалентно аксиоме выбора, если что

[Munin]

nya в сообщении #1324531 писал(а):

Недостаточно, я же уже говорил в этой теме, что Z/4Z не получить таким образом.

Я думал, что это пример расширения, но не думал, что нельзя получить другими способами. Спасибо за уточнение.

[vpb]

Вот некоторые основные понятия, относящиеся к расширениям модулей и групп.

1) Пусть $R$ --- ассоциативное кольцо, $M_1$ и $M_2$ --- $R$-модули. Расширение $M_2$ с помощью $M_1$ --- это короткая точная последовательность $R$-модулей вида

$$ 0\longrightarrow M_1 \longrightarrow M \longrightarrow M_2\longrightarrow 0.$$

Также расширением $M_2$ с помощью $M_1$ называется средний модуль $M$, фигурирующий в этой последовательности. (А иногда говорят (в теории групп особенно) наоборот, что $M$ --- расширение $M_1$ с помощью $M_2$.)

Если имеется коммутативная диаграмма вида

$$ \xymatrix{ 0\ar[r] & M_1\ar[r]^{\alpha_1}\ar@{=}[d] & M \ar[r]^{\beta_1}\ar[d]^{\varphi} & M_2\ar[r]\ar@{=}[d] & 0 \\ 0\ar[r] & M_1\ar[r]^{\alpha_2} & M'\ar[r]^{\beta_2} & M_2\ar[r] & 0 } $$

то расширения, представленные строками этой диаграммы, называются конгруэнтными. Конгруэнтность расширений ---
отношение эквивалентности. См.Маклейн, Гомология, гл.3.

Множество классов эквивалентности расширений $M_2$ с помощью $M_1$ обозначается ${\rm Ext}_R(M_2,M_1)$. На самом деле, ${\rm Ext}_R$ --- первый из серии так называемых "когомологических функторов" ${\rm Ext}^n_R$, так что обычно пишется ${\rm Ext}^1_R$, а не просто ${\rm Ext}_R$.

На множестве ${\rm Ext}^1_R$ можно ввести некоторую операцию сложения, относительно которой оно является абелевой группой.

-- 20.07.2018, 01:39 --

2) Теперь обратимся к расширениям групп. Пусть $N$ и $H$ --- две группы. Расширение $H$ с помощью
$N$ --- это короткая точная последовательность групп

$$ 1\longrightarrow N \stackrel\alpha\longrightarrow G \stackrel\beta\longrightarrow H\longrightarrow 1$$

(или просто группа $G$, фигурирующая в этой последовательности). Аналогично случаю модулей, два расширения считаются эквивалентными, если существует коммутативная диаграмма вида

$$ \xymatrix{ 1\ar[r] & N\ar[r]^{\alpha_1}\ar@{=}[d] & G_1 \ar[r]^{\beta_1}\ar[d] & H\ar[r]\ar@{=}[d] & 1 \\ 1\ar[r] & N\ar[r]^{\alpha_2} & G_2\ar[r]^{\beta_2} & H\ar[r] &1 } $$

Обозначим множество классов эквивалентности расширений через $E(H,N)$. (Выше g______d обозначал это
множество через ${\rm Ext}(H,N)$. Но, кажется, по отношению к расширениям групп такое обозначение нигде не употребляется; главное же, что и само это множество не рассматривается, по причинам, которые будут объяснены чуть ниже. )

Множество $E(H,N)$ определяется "похоже" на то, как определяется ${\rm Ext}_R(M_2,M_1)$. Однако свойства
этого множества совершенно другие. Это не группа или что-то вроде, а просто множество. Поэтому изучать его "в целом"
было бы трудно. Его и не изучают. Ниже мы увидим, что изучать его в целом вообще нет необходимости. Тем не менее,
внутри него есть части, которые поддаются изучению.

-- 20.07.2018, 01:42 --

3) Напомним кое-что о группах. Пусть $G$ --- группа, и $g\in G$. Отображение $\varphi_g:x\mapsto gxg^{-1}$ --- автоморфизм группы $G$ (называемый внутренним автоморфизмом). $\varphi_g\varphi_h=\varphi_{gh}$, так что $g\mapsto\varphi_g$ --- гомоморфизм из $G$ в ${\rm Aut}(G)$. Ядро этого гомоморфизма есть $Z(G)$ (центр $G$), а образ обозначают ${\rm Inn(G)}$. Если $Z(G)=1$, ${\rm Inn(G)}$ можно отождествлять с $G$. Кроме того, всегда ${\rm Inn(G)}\trianglelefteq{\rm Aut}(G)$ ($\trianglelefteq$ --- знак нормальной подгруппы). Факторгруппа

$$ {\rm Out}(G)={\rm Aut}(G)/{\rm Inn}(G) $$

называется группой внешних автоморфизмов группы $G$.

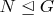
Более общо, пусть $N\trianglelefteq G$. Тогда $N$ инвариантна относительно всех $\varphi_g$. Поэтому имеется
гомоморфизм $\chi:G\longrightarrow {\rm Aut}(N)$. Ядро $\chi$ есть

$$ C_G(N)=\{ g\in G\mid gn=ng \ \forall \ n\in N\} $$

централизатор $N$ в $G$. В частности, если $C_G(N)=1$, то $G$ является подгруппой в ${\rm Aut}(N)$,
содержащей ${\rm Inn}(N)=N$.

Композиция $\chi$ с эпиморфизмом ${\rm Aut}(N)\longrightarrow {\rm Out}(N)$ дает гомоморфизм $\sigma:G\longrightarrow {\rm Out}(N)$. Легко понять, что $\sigma(N)=1$, так что $\sigma$ пропускается через
факторгруппу $G/N$, и получается гомоморфизм $\psi:G/N\longrightarrow {\rm Out}(N)$. В частности, когда $N$ абелева, имеем гомоморфизм $G/N\longrightarrow {\rm Aut}(N)$.

Теперь пусть

$$ 1\longrightarrow N \stackrel\alpha\longrightarrow G \stackrel\beta\longrightarrow H\longrightarrow 1$$

Отождествляя $N$ с $\alpha(N)\trianglelefteq G$ посредством $\alpha$, а $H$ с $G/\alpha(N)$ в силу $\beta$, видим, что последнее расширение индуцирует некоторый гомоморфизм $\psi:H\longrightarrow {\rm Out}(N)$. Легко видеть, что
для двух эквивалентных расширений гомоморфизм $\psi$ --- один и тот же т.е. определяется только классом
эквивалентности расширения.

Пусть ${\mathcal E}(H,N,\psi)$ --- совокупность классов эквивалентности расширений, отвечающих данному
$\psi:H\longrightarrow {\rm Out}(N)$. Отметим, что ${\mathcal E}(H,N,\psi)$ может быть пусто.
Тогда имеем разбиение

$$E(H,N)=\bigsqcup_\psi {\mathcal E}(H,N,\psi) $$

разбиение по всем $\psi\in{\rm Hom}(H,{\rm Out}(N))$. Множества ${\mathcal E}(H,N,\psi)$ --- это и есть
те "малые части" $E(H,N)$, которые допускают изучение.

-- 20.07.2018, 01:45 --

4) Пусть сначала $N$ абелева. Будем писать $A$ вместо $N$ в этом случае. Заметим, что в силу того, что $\psi$
--- гомоморфизм из $H$ в ${\rm Out}(A)={\rm Aut}(A)$, $A$ является (левым) $H$-модулем.

Тогда ${\mathcal E}(H,A,\psi)$ всегда непусто, так как содержит расширение

$$ 1\longrightarrow A \longrightarrow A\leftthreetimes H \longrightarrow H\longrightarrow 1$$

где $A\leftthreetimes H$ --- полупрямое произведение. Обычно считают $\psi$ уже заданным раз и навсегда, и в обозначениях $\psi$ опускают, пишут просто ${\mathcal E}(H,A)$.

На ${\mathcal E}(H,A)$ можно определить структуру абелевой группы, некоторым образом. Более того, эта группа изоморфна группе 2-когомологий

$$ H^2(H,A)=Z^2(H,A)/B^2(H,A), $$

где $Z^2(H,A)$ --- группа всех 2-коциклов, т.е. отображений $f:H\times H\longrightarrow A$, удовлетворяющих
условию

$$ xf(y,z)+f(x,yz)=f(x,y)+f(xy,z) \ \ \ \ \forall\ x,y,z\in H, $$

а $B^2(H,A)$ --- группа 2-кограниц, т.е. отображений $f$, имеющих вид

$$ f(x,y)= h(x)+xh(y)-h(xy) $$

для некоторого отображения $h:H\longrightarrow A$.

-- 20.07.2018, 01:48 --

5) Теперь рассмотрим случай, когда $N$ --- не обязательно абелева. Пусть $\psi:H\longrightarrow {\rm Out}(N)$.
Отметим, что ${\rm Inn}(N)$ действует тождественно на $C=Z(N)$, и поэтому $C$ является $H$-модулем. Поэтому
можно рассматривать группу 3-когомологий $H^3(H,C)$. Оказывается, что можно некоторым образом сопоставить
гомоморфизму $\psi$ класс 3-когомологий $\theta=\theta(\psi)\in H^3(H,C)$ таким образом, что ${\mathcal E}(H,N,\psi)$ непусто тогда и только тогда, когда $\theta(\psi)=0$. Кроме того, если $\theta(\psi)=0$, то множество ${\mathcal E}(H,N,\psi)$ можно перенумеровать элементами группы $H^2(H,C)$ (более точно, существует некоторое каноническое регулярное действие группы ${\mathcal E}(H,C)\cong H^2(H,C)$ на ${\mathcal E}(H,N,\psi)$.)

6) На самом же деле оказывается, что в рассмотрении групп 3-когомологий особой надобности нет (в задаче о строении групп; в других задачах, возможно, и есть). Поясним причину этого.

Будем рассматривать группы $G$ только конечные, или же бесконечные, но по крайней мере имеющие конечный
композиционный ряд. В любой такой группе $G$, очевидно, есть нетривиальная минимальная нормальная подгруппа $N$ (т.е. не существует нормальных подгрупп $N_1\trianglelefteq G$ таких, что $1<N_1<N$). Пусть $S$ обозначает подгруппу,
порожденную всеми минимальными нормальными подгруппами (т.наз. цоколь группы $G$).

Утверждение. Либо $G$ имеет нетривиальную абелеву нормальную подгруппу $A$, либо $C_G(S)=1$. В последнем случае $S=S_1\times\ldots\times S_l$, где $S_i$ --- некоторые минимальные нормальные подгруппы в $G$, и каждая $S_i$ имеет вид $T_i\times\ldots\times T_i$, где $T_i$ --- некоторая неабелева простая группа.
(Доказательство этого утверждения следует из результатов главы 8 в кн. М.Холл, Теория групп.)

Последнее утверждение может быть использовано для изучения строения групп следующим образом. Если в группе $G$
есть абелева нормальная подгруппа $A$, то ее строение определяется некоторым когомологическим классом
$\theta\in H^2(G/A,A)$ (мы предполагаем, что у нас уже есть некоторые сведения о группе $G/A$ и ее действии на $A$).
Если же абелевой нормальной подгруппы нет, то $C_G(S)=1$, откуда $G$ есть некоторая подгруппа в ${\rm Aut}(S)$, содержащая $S$ в качестве нормальной подгруппы и, таким образом, восстанавливающаяся по группе $G/S$, которая является подгруппой в ${\rm Out}(S)$ (а последняя группа сравнительно несложно описывается).

-- 20.07.2018, 01:51 --

7) Следует сделать еще одно замечание. Разные классы когомологий из $H^2(H,A)$ соответствуют, по определению,
неэквивалентным расширениям

$$ 1\longrightarrow N \longrightarrow G \longrightarrow H\longrightarrow 1$$

Но при этом "средние" группы $G$ могут оказаться изоморфными. Именно из-за этого феномена задача об описании всех непростых конечных групп фактически неразрешима.

Поясним последнее утверждение на пальцах. Опуская кое-какие мотивировки, опишем следующую конструкцию.

Пусть $p$ --- нечетное простое число, $A=Z_p^m$, $B=Z_p^n$. Пусть $f:B\times B\longrightarrow A$ --- билинейное
отображение (мы можем говорить о билинейных отображениях, так как оба $A$ и $B$ можно рассматривать как пространства над полем из $p$ элементов). Определим на множестве $G=A\times B$ умножение по правилу

$$ (a,b)(a_1,b_1)=(a+a_1+f(b,b_1), b+b_1). $$

Тогда можно проверить, что относительно этого умножения $G$ --- группа. Обозначим ее $G(f)$.

На пространстве всех отображений $f$ указанного типа действует группа $T={\rm Aut}(A)\times{\rm Aut}(B)$. Можно
показать, что если отображения $f$ и $f_1$ лежат в одной орбите относительно данного действия, то $G(f)\cong G(f_1)$. Более того, если оба $f$ и $f_1$ кососимметричны, ${\rm Ker\,}f={\rm Ker\,}f_1=0$ и ${\rm Im\,}f={\rm Im\,}f_1=A$ (где

$$ {\rm Ker\,}f=\{b\in B\mid f(b,b_1)=0\ \forall b_1\in B\}, \qquad {\rm Im\,}f=\langle f(b,b_1)\mid b,b_1\in B\rangle $$

то условие $G(f)\cong G(f_1)$ эквивалентно тому, что $f$ и $f_1$ лежат в одной орбите. Поэтому задача о классификации групп $G$ указанного типа с точностью до изоморфизма эквивалентна задаче о классификации отображений $f$ с точностью до действия группы $T$. А эта задача в случае, когда $m,n\geq3$, содержит в себе "задачу о паре матриц", и тем самым в определенном смысле неразрешима.

(Задача о паре матриц --- это задача о приведении пары матриц к каноническому виду одновременным преобразованием подобия:

$$ (X,Y)\sim (ZXZ^{-1}, ZYZ^{-1}). $$

Когда матрица одна, то ее можно привести к жордановой форме (над алгебраически замкнутым полем) или к канонической рациональной форме (над произвольным полем). Если же матриц две или больше, то разумного решения эта задача не допускает. Задача о паре матриц --- это эталонный пример "дикой" задачи, типа NP-полных задач
в теории сложности. Я с соответствующим концепциями едва знаком, поэтому точнее сказать не могу.)

[g______d]

vpb, спасибо за большую проделанную работу! Лично мне этот текст прояснил некоторые вещи, которые я понимал неправильно, и его просто приятно читать.

[пианист]

+1
Очень интересно и познавательно!

[Munin]

Восхитительно, но я перестаю понимать примерно на половине :-)

Есть куча вопросов:
0) где это почитать, поподробнее и попроще?

1) Как-то странно, что ${\mathcal E}(H,N,\psi)$ может быть пусто. Я думал, по данному $\psi$ всегда можно построить $N\leftthreetimes_\psi H.$ Можно привести простенький пример?

2) Почему 2-коциклы и 2-кограницы определяются таким образом, какую это имеет связь с коциклами и кограницами из алгебраической топологии?

3) Можно простенький пример неэквивалентных расширений с изоморфными $G$? Я помню, что где-то его видел, но пусть будет здесь ещё, чтобы не искать.