В статье вики по ссылке, как мне кажется, довольно подробно описано отношение эквивалентности на точных последовательностях. Или Вам нужно определение точной последовательности?
См. также Браун, "Когомологии групп" глава IV параграф 1 (определение расширения и отношения эквивалентности) или Маклейн "Гомология" глава IV параграф 3.
Используется ли где-то обозначение
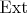
для множества классов эквивалентности всех расширений в неабелевом случае -- я с ходу не знаю, но не уверен, что это принципиальный момент.
Спасибо, но, боюсь, Вы меня неправильно поняли. Я не просил снабдить меня общими ссылками относительно теории расширений групп, на книжки или Интернет-ресурсы, так как мне этот предмет до некоторой степени неплохо известен. Я спрашивал, каков точный смысл и точная формулировка некоего предложения из поста
nya. Я даже намекал, что это предложение ошибочно, но этот намек не был понят. Видите ли Вы сейчас, в чем там ошибка ? (Вы, насколько я понимаю, специалист, и где там ошибка, должно быть очевидным, имхо.)



