Показать, что данная функция интегрируема на любом отрезке.

[bitcoin]

mihaild в сообщении #1308425 писал(а):

(откуда, кстати, вы взяли $\varepsilon \sum \Delta x_i \leqslant \varepsilon$? это правда, но нужно уметь это доказывать)

Так у нас ведь отрезок длиной $1$ рассматривается. А мы сделали разбиение и рассматриваем часть его, она уж точно меньше 1, верно ведь?

mihaild в сообщении #1308425 писал(а):

А вы посмотрите: удастся ли вам для любого числа $q$ подобрать такие $\varepsilon$ и $\delta$, чтобы итоговая оценка на колебание получилась меньше $p$?

Слету не получается увязать все эти буквы, нужно подумать

-- 28.04.2018, 20:32 --

Кстати, придумал получше оценку!

$\varepsilon\sum \Delta x_i\leqslant \varepsilon \left(1-\delta \cdot \left(\left[\dfrac{1}{\varepsilon^2}\right]+1\right)\right)$

Если для всех отрезков, то получается, что $\displaystyle\sum_{i}\omega_i\Delta x_i\leqslant \delta \cdot \left(\left[\dfrac{1}{\varepsilon^2}\right]+1\right)+ \varepsilon \left(1-\delta \cdot \left(\left[\dfrac{1}{\varepsilon^2}\right]+1\right)\right)$

-- 28.04.2018, 20:35 --

Так как $\varepsilon < 1 $ имеем:

$$\displaystyle\sum_{i}\omega_i\Delta x_i\leqslant \delta \cdot \left(\left[\dfrac{1}{\varepsilon^2}\right]+1\right)+ \varepsilon \left(1-\delta \cdot \left(\left[\dfrac{1}{\varepsilon^2}\right]+1\right)\right)<\varepsilon \delta \cdot \left(\left[\dfrac{1}{\varepsilon^2}\right]+1\right)+ \varepsilon \left(1-\delta \cdot \left(\left[\dfrac{1}{\varepsilon^2}\right]+1\right)\right)=\varepsilon$$

Верно ли это?

-- 28.04.2018, 20:43 --

Даже, если это окажется верным, остается тогда вопрос, а что будет, если мы возьмем $\varepsilon$ вне интервала $(0;1)$? Ведь тогда у нас эта схема не будет работать....

[mihaild]

bitcoin в сообщении #1308427 писал(а):

$\varepsilon\sum \Delta x_i\leqslant \varepsilon \left(1-\delta \cdot \left(\left[\dfrac{1}{\varepsilon^2}\right]+1\right)\right)$

Эта оценка неверна: у нас же отрезки, на которых $w_i$ большое, могут быть и сильно короче $\delta$. Но она и не нужна.

Итак, у нас получается, что для любого $\delta$ для любого разбиения радиусом не больше $\delta$ и для любого $\varepsilon$ выполнено $\sum w_i \Delta x_i \leqslant \varepsilon + \delta \left(\frac{1}{\varepsilon^2} + 1\right)$.
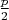
Теперь мы хотим подобрать $\varepsilon$ и $\delta$ так, чтобы получилось $\varepsilon + \delta \left(\frac{1}{\varepsilon^2} + 1\right) \leqslant p$. Как это сделать? Ну давайте попробуем сделать так, чтобы каждое слагаемое слева не превосходило $\frac{p}{2}$. Это возможно?

bitcoin в сообщении #1308427 писал(а):

Даже, если это окажется верным, остается тогда вопрос, а что будет, если мы возьмем $\varepsilon$ вне интервала $(0;1)$? Ведь тогда у нас эта схема не будет работать....

Наша оценка останется верной: она основывалась только на том, что отрезков точек, в которых $w_i > \varepsilon$, не слишком много, а в остальных $w_i$ не слишком большое. У нас конечно получится что-то не очень интересное - $\sum w_i \Delta x_i \leqslant \text{что-то большее 1}$, но это верно.

[bitcoin]

Можно взять $\varepsilon=\dfrac{p}{4}$, $\delta=\dfrac{p^3}{16+4p^2}$, тогда будет выполняться неравенство. Правильно ведь?

[mihaild]

Да, правильно. Таким образом, для любого $p$ можно указать $\delta$ такое, что при любом разбиении с радиусом меньше $p$ колебание на $[0; 1]$ будет меньше $\delta$. Что собственно и является достаточным условием интегрируемости на $[0; 1]$.
Осталось только доказать интегрируемость на любом другом отрезке, это можно сделать несколькими несложными способами.

[bitcoin]

Спасибо, понятно, разобрался!!! Понимаю, как провести рассуждения для отрезка $[a;b]$, хотя бы просто повторить те же самые рассуждения, только длина отрезка будет $b-a$.

[ewert]

bitcoin в сообщении #1307656 писал(а):

$\omega_i=M_i-m_i$ --колебание $f(x)$

Колебания здесь вредны. Тут всё грубее: мы же уверены, что интеграл есть ноль -- так надо тупо и доказывать, что интегральные суммы стремятся к нулю.

(Оффтоп)

mihaild в сообщении #1307657 писал(а):

(вы знаете критерий Лебега интегрируемости по Риману? если да, то всё совсем просто)

(эта задачка рассчитана в точности на обход критерия Лебега. Т.к. сия артиллерия тяжела, доказать же нетрудно и вполне элементарно)

Тупо по любому эпсилону берём сперва $n>\frac2{\varepsilon}$. Точек со знаменателем, меньшим $n$, будет всяко уж меньше, чем $n^2$. Ну так и выберем ранг дробления $\delta=\frac{\varepsilon}{2n^2}$, вот и всё.

-- Ср май 02, 2018 16:36:08 --

bitcoin в сообщении #1308449 писал(а):

Понимаю, как провести рассуждения для отрезка $[a;b]$, хотя бы просто повторить те же самые рассуждения, только длина отрезка будет $b-a$.

Это, кстати, лишнее. Если есть интегрируемость на $[0;1]$, то по свойству аддитивности она есть и на любом целочисленном отрезке, а тогда и вообще на любом как части целочисленного.