Если мы рассмотрим в СТО одного наблюдателя, который мог бы мгновенно получать информацию обо всем в своем пространственном срезе, это бы не привело ни к каким же временным парадоксам?
В отличии от двух таких наблюдателей, которые могли бы таким образом обмениваться сверхсветовыми сигналами.
Математически это можно попробовать записать примерно так. Пусть этот самый наблюдатель движется согласно следующему уравнению:

Здесь

- времениподобное нигде не особое векторное поле (четырёхскорость наблюдателя):

Обозначим символом

трёхмерное пространственное слоение трансверсальное

. Каждый его слой как раз и является трёхмерным пространством означенного выше наблюдателя. По определению, трёхмерная метрика в слоении

:

Теперь запишем следующее замечательное уравнение:

Пусть в некоторой области пространства-времени поле

, тогда там уравнение (4) имеет вид обычного волнового уравнения (Д’Аламбера):

То есть в этой области пространства-времени поле
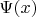
является обычным волновым полем распространяющимся со скоростью света.
Пусть в некоторой другой области пространства-времени поле

, тогда там уравнение (4) имеет вид обычного уравнения Лапласа для слоения

:

То есть в этой области пространства-времени, в трёхмерном слое

поле
 распространяется мгновенно
распространяется мгновенно (как Ньютоновский гравитационный потенциал удовлетворяющий уравнению Лапласа, а не уравнению Д’Аламбера).
Если вдруг кому не лень, то можете записать Лагранжиан из которого можно получить уравнение (4).



