Помогите, пожалуйста, разобраться в двух упражнениях из учебника А.Т.Фоменко "Курс гомотопической топологии". Все мои попытки, к сожалению, были разбиты в пух и прах при их проверке, а теории из данного учебника не хватает для глобального понимания задач.
Топология на

введена следующим образом: множество

замкнуто тогда и только тогда, когда все пересечения
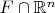
замкнуты в своих пространствах

1) Покажите, что последовательность

точек пространства

имеет предел тогда и только тогда, когда последовательность

- финитна.
2) Покажите, что пространство

не метризуемо.
В первой задаче пытался думать следующим образом, но думаю, что это в корне неверно, т.к я у элемента пространства пытаюсь найти его составляющие и получается "последовательность последовательностей":
Все

и т.д есть подпоследовательности какой-либо последовательности

. Логично подумать (?), что последовательностью состоящей из последовательностей

и т.д есть финитная последовательность

. А если

сходится сама к себе, то все ее подпоследовательности сходятся к

.
Также я немного рассуждал о самих точках последовательности:
Можно ли из каждой точки, после

-того элемента (ненулевого) "отбросить" все нули? Тогда мы получим, что:
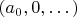
- образ точки из

.
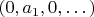
- образ точки из

.
и т.д
А

есть индуктивный предел

Так что что-то похожее, вроде есть..
Также ясно, что немного условие можно переформулировать, т.к
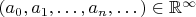
. Т.е слово "финитна" говорит нам о том, что эта последовательность является элементом пространства

.
Вообще, мне кажется, моя ошибка заключается в том, что я пытаюсь мыслить некоторые эквивалент поточечной сходимости, хотя гораздо лучше было бы попробовать определить сходимость исходя из данной топологии и попробовать увидеть связь.
Заранее, спасибо!



