Если последовательность стремится к бесконечности, что можно сказать про любую её подпоследовательность?
Она тоже стремится к бесконечности.
Все, у меня "щелкнуло", и теперь мне стыдно за такие глупые вопросы. Большое Вам спасибо! Почему-то у меня в голове перемешались определения неограниченной и стремящейся к бесконечности последовательностей (точно так же, как когда-то ранее я путал наличие у последовательности предельных точек и сходимости).
Видимо, пришла пора устроить себе небольшое самотестирование по всему пройденному (обычно провожу их после каждых 1-3 листков).
Вот здесь лучше было строить противоречие.
Ваши выкладки мне понятны, но чем они лучше чем моей отсылки к задаче 12 листка 11 -- не понятно.
-- 09.02.2018, 14:13 --Вот новое исправленное доказательство 14.а с учетом замечаний
ewert и других.
Задача 14.
Пусть функция

непрерывна на отрезке
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
. Доказать, что
а) функция

ограничена на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
;
Произвольная последовательность

из чисел отрезка
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
ограничена, и значит имеет хотя бы одну предельную точку

(задача 13 листка 11). Пусть

-- сходящаяся к

подпоследовательность

. По определению непрерывности функции в точке, последовательность

сходится к

. Из сходимости подпоследовательности

следует, что вся последовательность
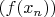
не является стремящейся к бесконечности.
Таким образом, какова бы не была последовательность

, последовательность
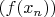
не стремится к бесконечности. Отсюда следует ограниченность

на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
.



