grizzlyспасибо, кажется догадался.
Задача 14.
Пусть функция

непрерывна на отрезке
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
. Доказать, что
а) функция

ограничена на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
;
Доказательство.
От противного. Предположим, что

не ограничена на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
, т.е.
![$\forall C\ \exists x\in[a,b]\ |f(x)|>C$ $\forall C\ \exists x\in[a,b]\ |f(x)|>C$](https://dxdy-02.korotkov.co.uk/f/1/8/2/182ebf1bc9cccdf2ad98a2baf43143dc82.png)
.
Пусть

-- последовательность из чисел отрезка
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
такая, что последовательность
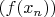
стремится к бесконечности.
Последовательность

ограничена, и значит имеет более одной предельной точки (задача 13 листка 11).
Возьмем произвольную предельную точку

последовательности

, и пусть
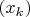
-- сходящаяся к

подпоследовательность

. По определению непрерывности функции в точке, последовательность

сходится к

и, следовательно, ограничена (задача 12 листка 11).
За вычетом сходящихся подпоследовательностей, в

останется не более конечного числа членов. Конечное число соответствующих значений

ограничено.
Таким образом, последовательность
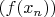
ограничена.
Полученное противоречие доказывает ограниченность

на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
.