векторы
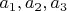
линейно зависимы, если существуют такие

, что справедливо равенство:

. По условию, система векторов линейно зависима. Если попытаться выразить

, получим

. Получается,

не выражается, если его множитель равен 0. Но в таком случае можно записать

, далее, поделив обе части на

, получим

. Поправьте если где ошибка
,
всё правильно, только недостаточно аккуратно. Вы пропускаете логические связки и т.д. Сейчас я Вам, для примеру, покажу, как можно написать более аккуратно. При этом, для понятности, я буду писать с
преувеличенной (и сильно!) аккуратностью, которой в реальности от Вас не требуется. Причем буду писать нарочито суконным языком.
Определение. Векторы

,

,
 линейно зависимы
линейно зависимы, если существуют
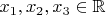
, не равные одновременно нулю и такие, что

.
Определение. Векторы

и
 отличаются множителем,
отличаются множителем, если существует

такое, что
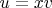
, или существует

такое, что

.
Определение. Вектор
 выражается через
выражается через  и
и  ,
, если существуют

,

такие, что
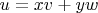
.
Утверждение. Если векторы

,

и

линейно зависимы, и

не выражается через

и

, то

и

отличаются множителем.
Доказательство. Существуют

,

,

такие, что
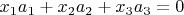
, причем не все

,

,

равны нулю. Допустим, что
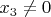
. Перенеся
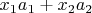
в правую часть и поделив соотношение на

, получим
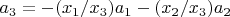
. Значит,

выражается через

и

, что противоречит условию. Поэтому

. Следовательно,

. Кроме того, по крайней мере одно из

и

отлично от нуля. Допустим, что

. Тогда
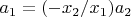
, значит

и

отличаются множителем. Аналогично рассуждаем в случае, когда

.
Утверждение доказано.
Первая Ваша попытка --- это была, скажем так, чепуха, вторая --- на "4 с плюсом" по пятибалльной системе.
В общем, читайте учебники, другие книжки, журналы "Квант", смотрите как люди пишут, со временем и сами научитесь.



