Доказать что прамая

пересекает стороны

и

Ну тут можно вашим методом.
Допустим

равнобедренный,

Тогда центры обоих окружностей лежат на медиане-биссектрисе-высоте
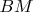
, причем

<

.

проходит через

и

.
Зафиксируем точки

и

, а точку

передвинем в точку

вдоль прямой

так что

, но по-прежнему

<

. Тогда получим треугольник в котором

, в котором построим описанную и вписанную окружности с центрами

и

Точки

и

будут принадлежать к серединному перпендикуляру к

, общему для обоих треугольников, а точки

и

будут принадлежать к биссектрисе угла

, тоже общей для обоих треугольников.
Обозначим как

точку пересечения указанных серединного перпендикуляра к

и биссектрисы угла

.
Точки

и

будут принадлежать отрезкам

и

соответственно до тех пор пока

. Ну а

будет между

и

потому что она лжит на серединном перпендикуляре к

, а он подвинется вправо на

. А

будет между

и

потому что угол

, а

лежит на биссектрисе угла

Ну и из этого очевидно что прямая

будет пересекать стороны

и

(Картинка)
А... нет. Еще надо доказать что проекция

на

всегда будет правее проекции

на

.



