Всё здорово,остроумно, но слишком поверхностно:нет желания вглядеться в цифры,подумать.Думаю,что заданные вопросы разрешаться по мере дальнейшего анализа таблицы.
Первое,что бросается в глаза-почти регулярное повторение последнего члена соседних разложений. Таблица,как бы расслаивается,распадается на две.Давайте так и сделаем:









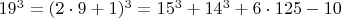



















О выделенных строчках я скажу позже.Посмотрим,по каким признакам произошёл распад.В левой таблице - разложение нечетных чисел с нечётным основанием:

В правой - разложение нечётных чисел с чётным основанием:

О чём это говорит?В этой связи,думаю,надо вспомнить,те формулы разложения кубов по квадратам,что были получены мной с помощью внутренней структуры кубов и приводились в моём раннем сообщении.
asta писал(а):
Почему это 4, а не 8? Разве не удобнее разложить куб на восемь угловых кубов и симметричную сердцевину?
krestovski писал(а):
Вот скажите честно, - в результате всех сделанных Вами преобразований для получения этих двух соотношений, Вы что-то новое узнали о кубах? -
Уважаемый krestovski и уважаемый lasta !Спасибо Вам за Ваши развёрнутые ответы.Особое спасибо Вам,уважаемый krestovski .за этот вопрос.Это - главный вопрос,который сразу,как лакмусовая бумага,выявляет цену сути всех заявлений и творений.Хорошо бы ,если бы каждый сам себе почаще задавал подобный вопрос.Хотя, Великая теорема Ферма-явление уникальное.Она не только имеет большое значение в науке,как катализатор новых идей,но и давно приобрела большое социальное значение:благодаря простоте и красоте свое формулировки она,как Храм,куда на равных приходят и академик и зубной техник,чтобы прикоснуться к великому и вечному,почувствовать себя приобщенным к творчеству великих умов человечества.Просто они часто путают свои личные победы и достижения с действительно таковыми,и спешат вынести их на всеобщее обсуждение.
Теперь по сути...Честно,так честно...На этом форуме,кроме основной задачи,у меня была ещё и сверх задача: выяснить вопрос - насколько уникальна сделанная мной расшифровка внутренней структуры кубов.Я получил явный вид того ,что скрывает в себе формула

.В каждом сообщении я твердил о внутренней структуре кубов, "мозолил" глаза этой формулой,что бы узнать - знает ли кто нибудь её расшифровку.Привёл явную подсказку - выражение

,шестая часть которого давно известна в математике и имеет своё название.Акцентировал внимание на на коэффициенте 4, роль которого была бы сразу понятна,знающим явный вид внутренней структуры куба.Теперь я убедился,что это действительно никому не известное ,уникальное знание и хотел бы впервые представить формулы явного вида внутренней структуры кубов здесь на этом форуме.Уверен,что впереди у них долгая и счастливая жизнь в математике.Вот они:
![$$X^3= (2a+1)^3 = 6[2^2 +4^2 +6^2+8^2 +.......+ (2a)^2] +(2a+1)$$ $$X^3= (2a+1)^3 = 6[2^2 +4^2 +6^2+8^2 +.......+ (2a)^2] +(2a+1)$$](https://dxdy-02.korotkov.co.uk/f/5/a/d/5ade0139ddc24cacc4378b880872a19182.png)
,где

-целое число
![$$Y^3= (2a)^3 = 6[1+3^2 +5^2 +7^2+9^2 +.......+ (2a -1)^2] +(2a)$$ $$Y^3= (2a)^3 = 6[1+3^2 +5^2 +7^2+9^2 +.......+ (2a -1)^2] +(2a)$$](https://dxdy-03.korotkov.co.uk/f/6/4/1/641f90b01ee53a45764171e3a103d5bf82.png)
,где

-целое число.
Согласитесь - красивые формулы.Теперь Вы видите откуда берется 4 в разложении нечётных кубов и,что никакая 8 или другое чётное число там быть не может.
Эти формулы говорят нам о том,что в мире кубов существует асимметрия по отношению к кубам разной четности и она связана с их внутренней структурой.И теперь,мы видим,что эта асимметрия существует и в кубах чисел одной четности,но с разными по чётности основаниями. По видимому,эта закономерность более глубокая и,может быть,именно она не даёт нам возможность применить "метод бесконечного спуска",так хорошо работающий для чётных с чётным основанием степеней, для степеней нечётных.
Теперь-самое главное. о чем нам говорят эти таблицы разложений на соседние кубы.В физике есть такое понятие,как"неустойчивое или возбуждённое состояние тела".Шарик на вершине горки находиться в неустойчивом состоянии,поскольку обладает избытком потенциальной энергии.Атом,поглотивший квант света,находиться в возбуждённом состоянии из которого обязательно перейдет в устойчивое,испустив этот квант.Все разложения в рассматриваемой таблице (а точнее- в двух таблицах) в не выделенных строчках - это неустойчивые разложения,разложения не окончательные.
Разложение на соседние кубы и просто остаток- молоинформативно. Нас ещё интересует - а окончательное ли это разложение?Поскольку единичное приращение куба - число всегда кратное

плюс 1 ,поэтому,зная особенность любого разложения кубов по последнему члену,мы прибавляем к нашему остатку этот член и делим полученное число на

.Если разложение выполнено верно,то результатом деления всегда будет целое число.Именно это я имел в виду,когда говорил о первой особенности разложений .
Так вот в разложениях, которые не выделены,остаток больше единичного приращения младшего куба.Но это ведь соседние кубы.С учётом этого,таблицы разложения будут следующие:





























Получается,что у кубов некоторых нечётных чисел нет разложения на соседние кубы.



