школьная геометрия *

[fred1996]

grizzly в сообщении #1271376 писал(а):

Красивая задача. Насколько просто доказывается, что у прямоугольного треугольника углы равны и насколько сложнее -- обратная задача. Всё никак не покидает ощущение, что можно поискать простое рассуждение и в обратную сторону. Идея fred1996 мне нравится и она превращает задачу в хороший пример полезности методов анализа в геометрии.

(Оффтоп)

Когда-то в школе мне нравилась геометрия. Но потом на долгие годы я про нее забыл.
А потом как-то разговаривал с одним учителем математики, он мне и говорит, что мол в геометрии уже давно победили алгебраисты, и что мол сейчас всю геометрию доказывают с помощью анализа. Я, честно говоря, тогда не совсем понял его. А сейчас, когда начал наталкиваться на задачи по геометрии на этом форуме, понял, что геометрически совершенно разучился их решать. И все пытаюсь решить их аналитически, как в физике. Теперь я кажется понял ту сентенцию учителя математики.

[wrest]

pcyanide в сообщении #1271918 писал(а):

Если треугольник прямоугольный, то М - центр описанной окружности, то есть MA, MB и MC равны. Не вижу пока способ доказать это равенство.

Какое именно?
$MA=MC$ по определению медианы. $MB=MC$ доказывается элементарно достройкой прямоугольного треугольника $ABC$ до прямоугольника $ABCE$ ($AB$ параллельно $CE$ и $BC$ параллельно $AE$), тогда $AC$ и $BE$ диагонали, которые в прямоугольнике равны, пересекаются в точке $M$ и этой точкой делятся пополам.

[Skeptic]

Используя условия задачи, построить заданный треугольник невозможно. Необходимо ещё одно из его свойств. Это свойство задано в виде предполагаемого ответа: $\angle ABC$ прямой.
Естественно искать решение для прямоугольного треугольника, используя его свойства.

[grizzly]

Skeptic в сообщении #1271937 писал(а):

Используя условия задачи, построить заданный треугольник невозможно.

Вы не поняли. Это задача не на построение. Вообще не нужно ничего строить. Дан треугольник, у которого указанные углы равны. Нужно только доказать, что этот треугольник обязан быть прямоугольным. И даже тогда Вы его не сможете построить, потому что таких треугольников о-очень много разных.

[wrest]

Skeptic в сообщении #1271937 писал(а):

Используя условия задачи, построить заданный треугольник невозможно.

В смысле невозможно?
1. Строите прямую $b$
2. На прямой $b$ выбираете две точки $D$ и $M$
3. Из точки $D$ восставляете перпендикуляр и на этом перпендикуляре отмечает точку $B$
4. Соединяете точки $B$ и $M$
5. Строите биссектрису угла $\angle DBM$ и на её пересечении с прямой $b$ отмечаете точку $K$.
6. Строите окружность с центром в точке $M$ радиусом $MB$, на пересечении окружности и прямой $b$ отмечаете точки $A$ и $C.
7. Соединяете точки $A$ и $B$ а также точки $B$ и $C
8. Треугольник $ABC$ построен.

[Skeptic]

grizzly, это вы не понимаете, что геометрия - это, прежде всего, чертёж, который надо построить.


wrest, вы строите треугольник в предположении, что он прямоугольный. А в задаче это надо доказать. Т.е. вы используете ответ, как недостающее свойство треугольника. О чём я и писал. Попробуйте построить нужный треугольник, исходя только из заданного равенства углов, не привлекая его прямоугольность.

Я из ответа, что треугольник прямоугольный, решаю задачу.

[wrest]

Skeptic в сообщении #1272152 писал(а):

Попробуйте построить нужный треугольник, исходя только из заданного равенства углов, не привлекая его прямоугольность.

Задано не только равенство углов, но и то что эти углы образуют медиана (а значит задано равенство некоторых отрезков) и высота (а значит задан некий угол который прямой). Вот эти условия я использую при построении также как и условие равенства углов.

Skeptic в сообщении #1272152 писал(а):

Я из ответа, что треугольник прямоугольный, решаю задачу.

Ну вы решаете обратную задачу, как тут уже говорилось. Если треугольник $\triangle ABC$ прямоугольный, то медиана равна половине гипотенузы а из этого немедленно следует, что треугольник $\triangle BMC$ равнобедренный и так далее.
Прямая задача тут доказать что если медиана равна половине стороны на которую она опущена то треугольник необходимо прямоугольный. Это тоже быстрый путь к решению исходной задачи.
Предположим, что доказано, что и из $BM=\frac{1}{2}AC$ следует, что угол $\angle ABC$ прямой (сможете доказать?).
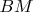
Тогда, поскольку углы $\angle ABD=\angle MBC$ по условию задачи, а углы $\angle ABD = \angle BCD = \angle BCM$ из подобия прямоугольных треугольников $\triangle ABD$ и $\triangle BCD$, то углы $\angle MCB = \angle MBC$ и треугольник $\triangle MBC$ равнобедренный, с равными сторонами $MB=MC$, а поскольку по условию задачи $BM$ медиана то $AM=MC$ и выходит что $BM=\frac{1}{2}AC$ а так может быть только если угол $\angle ABC$ прямой, ЧТД.

[grizzly]

Skeptic в сообщении #1272152 писал(а):

grizzly, это вы не понимаете, что геометрия - это, прежде всего, чертёж, который надо построить.

Надо же, а я всегда думал, что геометрия -- это прежде всего участок земли, который нужно измерить / поделить.

[arseniiv]

(Можно я побуду кэпом? Ну пожаалуйста. )

Skeptic в сообщении #1272152 писал(а):

это вы не понимаете, что геометрия - это, прежде всего, чертёж, который надо построить

Если предполагать, что каждая задача требует обязательно построения точного чертежа, возникает куча ерунды: (1) интересующий объект может быть не единственно возможным, в том числе их может быть континуум, даже если брать их с точностью до движения; (2) интересующий объект может быть трёхмерным (или это неестественное понимание задач, раз оно не обобщается на евклидовы пространства других размерностей и в том числе рассматриваемую в школе стереометрию); (3) построение может быть невозможно имеющимися ресурсами (время, знания, инструменты).

И это всё, конечно, глупости, ибо главный и нулевой аргумент в том, что если задача на доказательство/вычисление, она вообще не может быть решена черчением чего-либо. Эскизные чертежи используются для помощи голове увидеть путь — точные помогут ей для таких целей качественно не больше.