А можно не доказывать? Это очевидно

А чего спрашиваете, так или нет, если очевидно? Ну ладно, действительно очевидно.
-- Вс ноя 26, 2017 14:51:16 --Функцию

раскладываем по собственным функциям оператора Лапласа с учётом того, что решается задача

, где
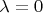
, что приводит к ряду
Ответ, вроде, правильный, но логика немного хромает. Собственные функции лапласиана тут ни при чем (да они и другие, как мы раньше видели). Просто раскладываем в ряд Фурье по синусам и получаем уравнение Бесселя (модифицированное) и неоднородное гранусловие к нему.
-- Вс ноя 26, 2017 14:57:58 --Функцию

раскладываем по собственным функциям оператора Лапласа
То же самое. Тут собственные функции ТОЛЬКО радиальной части оператора Лапласа (т.е. круглые бессели, обращающиеся в ноль на границе). А дальше получается уравнение на

и ненулевые гранусловия к нему.
___________________________________________
Да, интегралы получились гадкие, печально. В общем с интегралами проблема. Для конкретных параметров можно, конечно, подобрать какие-нибудь разумные аппроксимации функции источника, разбив интеграл интегрирования на подходящие куски (на всем интервале аппроксимацию, такую чтобы интеграл взялся, причем для любого

, не сделать, а на достаточно малом на куске --- почему бы и нет). Но в общем случае... не знаю как победить.
_____________________________________________
Ну ладно. Теперь обещанный другой вариант. Впрочем, судя по всему, там тоже интегралы будут гадкие.
У нас есть решение в виде ряда (по первому варианту, или по второму --- можно и то и другое взять). Проблема, как уже говорилось, в том, что сингулярность решения обеспечивается расходимостью рада, а тогда рядом с точкой сингулярности ряд сходится, но плохо. Улучшить ряд можно вполне очевидным способом. Пусть исходный ряд это

Здесь под индексом

можно понимать и пару индексов, что были в самом первом решении (разложение по собственным функциям), я буду рассуждать в обобщенном виде, не конкретизируя является ли индекс

одним числом или парой чисел.
Вид сингулярности нам известен, это то же самое, что в свободном пространстве. Пусть, как и раньше, решение для сободного пространства это

. Теперь делаем такой очевидный трюк:

и последнее слагаемое раскладываем в такой же ряд:

Здесь коэффициенты

можно записать в явном виде, как интегралы.
Тогда

Здесь ряд уже лучше сходится, ибо сингулярности в нем нет.
-- Вс ноя 26, 2017 15:28:03 --Ну, самое простое. Вблизи


Наоборот далеко

Ну а в двух промежуточных областях это примерно (грубо) константы (две разные). Итого пять интервалов на которых интеграл можно взять. Вот только

вызывает сомнение... Впрочем, а чего сомневаться. По частям и получается интегральный косинус. А это уже стандартная функция.
Если хочется поточнее, без таких резких изломов, то в промежуточной области аппроксимировать параболой. Интеграл тоже берется, а области с другим поведением можно отодвинуть подальше (значит будет точнее). Тут, конечно, интересный вопрос как именно делить на эти интервалы. В принципе, целое исследование на эту тему можно забубенить. Ну а если по простому.... Рисуем графики точного выражения и аппроксимации и подбираем на глаз, эмпирически

Чтобы это сделать разом, для любого

, перейти от

к переменной

.