Найдите наибольшее ландышевое число

[wrest]

Dmitriy40 в сообщении #1261142 писал(а):

Ведь "100 студентов различного возраста" не обязательно равно "100 студентов ВСЕ различного возраста", понятие "различного возраста" не требует уникальности возраста, требует лишь неодинаковости возраста у всех вообще.

Вот поэтому когда хотят чтобы уникальность появилась, к "различного" слева добавляют "попарно" :)

[gris]

Это в быту нужно уточнять, а в математике не нужно.
Вот задача: Некто написал на досце три различных натуральных числа.
Нешто Вы предположите, что он мог написать тройку и две двойки?
Если уж так невмоготу, то давайте введём камышовые числа.

[Ktina]

Dmitriy40 в сообщении #1261142 писал(а):

Ktina в сообщении #1261140 писал(а):

Станете ли Вы утверждать, что самому страшему из студентов не менее 99 лет?

Нет, но возраст и не выражается лишь натуральным числом. А если бы выражался - то да, стал бы.
Ну и Вы тут уже не употребили слова "попарно" (различного возраста).

Пусть под возрастом мы подразумеваем количество полных лет, прожитых человеком. В городе живут 40 тысяч человек различного возраста. Вы по-прежнему будете воспринимать "различного" как "попарно"?

[Dmitriy40]

Ktina
Вот потому и пытаюсь обращать Ваше внимание чтобы точнее формулировали свои задачи. Они интересные, но много сформулировано довольно небрежно (многосмысленно).

[wrest]

gris в сообщении #1261149 писал(а):

Вот задача: Некто написал на досце три различных натуральных числа.
Нешто Вы предположите, что он мог написать тройку и две двойки?

В варианте "три неравных числа" -- да, можно понять как тройка и две двойки :)
Но ведь "различный" это то же, что и "неравный"?

[Dmitriy40]

wrest в сообщении #1261156 писал(а):

Но ведь "различный" это то же, что и "неравный"?

Похоже только для двух элементов, если их больше - возникают варианты смысла. Во всяком случае в языке, как там принято в математике я не уверен.
(Хотя для меня "сто различных чисел" эквивалентно "все сто чисел разные", т.е. нет ни одного совпадения среди всех ста чисел.)

[gris]

wrest, "неравных" вообще слово не математическое. Можно сказать: "три не равных нулю числа", "три не равных друг другу числа" (пресловутая попарность). А вот "неравных" не встречал
Разве что у школоты: разделим отрезок на три неравных отрезка. И то, предполагается это ваше попарное неравенство. А кто умничать станет, тому Порция Лоз объяснит.

[Dmitriy40]

(Школота?!)

gris в сообщении #1261162 писал(а):

Разве что у школоты: разделим отрезок на три неравных отрезка.

Ну прям уж. В школьной геометрии точно так говорили. В обычной средней, не для школоты.

[gris]

(Оффтоп)

Dmitriy40, ну это я так, стилизуюсь под бывалого фидошника . Конечно, "в школьных задачниках и заданиях ЕГЭ".

[wrest]

Dmitriy40 в сообщении #1261161 писал(а):

Похоже только для двух элементов, если их больше - возникают варианты смысла.

Потому что только равенство транзитивно всегда (или мне неизвестны случаи когда это не так), т.е. если $a=b$ и $b=c$ то $a=c$
Так что три равных (одинаковых) числа или объекта это всегда три попарно равных (одинаковых) числа или объекта.
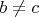
Другие отношения могут быть не транзитивны, например в известном множестве "камень ножницы бумага" отношение между элементами "превосходит" не транзитивно. Если обозначить отношение "превосходит" знаком $>$ а камень ножницы бумагу обозначить буквами $a$, $b$ и $c$, то из $a>b$ и $b>c$ не будет следовать $a>c$. Неравнество тоже не транзитивно, то есть из $a\ne b$ и $b\ne c$ не следует $a \ne c$

gris в сообщении #1261162 писал(а):

"неравных" вообще слово не математическое.

Я вам верю. А чтобы подзакрыть вопрос, какие термины отношений математичесие а какие нет -- "одинаковый", "равный", "различный", "разный", "неравный", "не равный", "такой же", "другой". В частности, как правильно "три разных" или "три различных" и есть ли разница?

-- 01.11.2017, 13:14 --

gris в сообщении #1261162 писал(а):

Разве что у школоты: разделим отрезок на три неравных отрезка. И то, предполагается это ваше попарное неравенство.

Хорошо, а как правильно сказать, что разделим отрезок длиной семь так что возможно будет тройка и две двойки?
"Разделим отрезок на три равных части" - не подходит. "Разделим отрезок на три неравных части" - тоже не подходит.
А... я понял! Просто пишем "Разделим отрезок на три произвольных части"?

[gris]

wrest, обсуждение в данной теме давно перешло на шутошный лад, так что я уж не стану развивать (разжигать) далее Конечно, не стоит разделять все слова на математические и не математические и требовать строгого определения слов "рассмотрим", "нетрудно показать" и прочих. Обычно всегда из контекста можно понять, что хотел сказать автор. Но нетрудно показать, что на пустом месте можно раздуть целую дискуссию.
Ну просто меня раздуло от гордости, что меня похвалили за нолик, и я решил поумничать. Или подурачиться. Иногда это не такие уж различные слова

Про отрезки. Я бы так сказал: "среди которых есть по крайней мере два неравных".

[Ktina]

(Оффтоп)

Ну, раз пошла такая пьянка, наливай, израильтянка пошёл такой жёсткий оффтоп, рискну задать вопрос: почему глазарно различных или головарно различных чисел не бывает, а вот попарно различные бывают?