Здравствуйте. Помогите пожалуйста разобраться с доказательством о распределении интенсивности от двух щелей в любой точке. В учебнике представлена такая фазовая диаграмма:

Далее приведено доказательство, но я ограничусь только тем, где необходимо пояснение. Здесь

и

- амплитуды, а

- разность фаз. Если щели освещены одинаково, то

. Из чертежа видно, что угол

равен
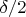
(можете подсказать, из какого закона это следует?), кроме того, видно также, что

( тут мне нужна помощь, я представлял это как равнобедренный треугольник с основанием

и одинаковыми углами

. А дальше по теореме косинусов ищем проекции и определяем результирующий вектор). Из этого уже следует определение о связи интенсивности света максимума с любой точкой. И подскажите ещё, я так понял, что интенсивность, например не максимума и минимума, а например половины от максимума и вообще в любой точке определяется именно определённым углом

,т.е. разностью фаз. Меня интересует как правильно посчитать интенсивность в любой точке. Спасибо за помощь.



