shwedka писал(а):
А все же как насчет положительных рецензий??? В третий раз прошу, а вы девушку игнорируете!!! Абидна, да???
А вот и "свисток":
Случаи 2 распадаются на два подслучая:
2a) на n делится число c
2b) на n делится число b.
Рассмотрим сначала
Случай 2a:

, но

≠

,

,

≠

, следовательно,

и

(см. 1*)
(6°) (здесь

и

).
Но нам понадобятся также и
(7°)

и

;
(8°)

и

.
Предварительно для удобства вычислений преобразуем

(следовательно и

) в 00001 с помощью некоторого

из Леммы 2*.
(9°) Теперь

, где
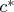
есть цифра

(см. 7°-8°).
Доказательство Случая 2а
(10°) В сумме P и Q (см. 7°-9°) 5-значное окончание равно 5-значному окончанию

, где пятая цифра, очевидно, не равна нулю. Запомним этот факт.
А теперь найдем 5-значное окончание этой суммы иначе (с учетом окончаний чисел

,

,

):
![$(P+Q)_{(5)} =
[(c^2+cb+b^2)+(c^2+ca+a^2)]_{(5)} =
[(2c^2)+c(b+a)+(b^2+a^2)]_{(5)} =
[(2c^2)+c(b+a)+(b^2+2ab+a^2)-2ab]_{(5)} =
[(2c^2)+c(b+a)+(a+b)^2-2ab]_{(5)} =
(2c^2)_{(5)}$ $(P+Q)_{(5)} =
[(c^2+cb+b^2)+(c^2+ca+a^2)]_{(5)} =
[(2c^2)+c(b+a)+(b^2+a^2)]_{(5)} =
[(2c^2)+c(b+a)+(b^2+2ab+a^2)-2ab]_{(5)} =
[(2c^2)+c(b+a)+(a+b)^2-2ab]_{(5)} =
(2c^2)_{(5)}$](https://dxdy-02.korotkov.co.uk/f/5/2/7/527a0a3119ab104bd2bc7f1ee514b36b82.png)
т.е. цифра

НЕ РАВНА НУЛЮ.
А теперь сравните этот результат с (10°).



