salangИсходную - это исходную. :( Что ж за горе-то. Это Ваша третья тема, посвященная чему-то похожему. Почему бы не сказать сразу, чего Вы хотите, почему из Вас это каждый раз по новой выбивать нужно. :(
Правильно ли я Вас понимаю, что Вам по какой-то причине понадобилось сложить два независимых нормальных распределения с расстоянием до нуля нормально распределенной точки
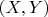
с независимыми компонентами, с разными, вообще говоря матожиданиями и дисперсиями? То есть - у всех четырех нормальных матожидание и дисперсия разные?
Так?
Если так, то вряд ли что-то у Вас получится. Вы пробовали хотя бы стандартное нормальное с распределением Рэлея сложить? Это для начала. А если с.к.о. нормального не равно параметру распределения Рэлея? А если еще теперь у нормального и матожидание ненулевое? (Все распределения независимы.)
Это все приличные вполне задачи, и в них съедобный ответ.
Хорошо, а если теперь просто стандартное нормальное попытаться сложить с распределением Райса? То, которое возникает на месте распределения Рэлея, если всего лишь сдвинуть матожидание? То есть распределение = стандартному сферическому+постоянный вектор. Получится?
----
Конечно, я сама придумала за Вас задачу, и если я сейчас занимаюсь задачей, не имеющей к Вашей никакого отношения, то угадайте с трех раз, кто за это отвечает.
----
Признаться, я не могу придумать мало-мальски реальное приложение необходимости работать с четырьмя нормальными распределениями, все из которых разные.



