Ни в коем случае!
Ну хорошо, тогда рассказываю. Для магнитного поля в области, где нет токов можно ввести скалярный потенциал

поскольку там ротор и дивергенция - ноль. Подробности - да хоть в Тамме. Тогда задача о диамагнетике сведется к задаче о диэлектрическом шаре в электрическом поле с той лишь разницей, что диэлектрическая проницаемость будет меньше единицы. Как мы тут установили, создать поле, которое стабилизирует шар в плоскости - дело не великое, поэтому сосредоточимся на вертикальной составляющей. Шар эквивалентен в первом приближении диполю, и по вертикали для
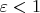
выталкивается убывающим полем. Приложив гравитационное поле мы можем стабилизировать шар в вертикальном направлении
не изменив наведенного дипольного момента. Всякое электрическое или магнитное поле момент изменит, причем сделает это так, что бы убить положение равновесия (в великие теоремы мы, все-таки, верим), а гравитационное поле независимо от электрического, и спокойно может нарушать всякие граничные условия электростатики. Математически задача сводится к тому, что бы так подобрать конфигурацию поля и форму тела, что бы где-нибудь квадратичная форма его вторый производных (гравитационное поле на них не влияет) оказалась положительно определенной (как только я это вспомнил, так сразу выяснил, что облажался с точечным зарядом), а потенциал в горизонтальной плоскости имел бы минимум (по вертикали в этом месте минимума, и вообще, экстремума, быть не может). Тогда гравитационным полем мы загоним туда и минимум по вертикальной оси. Доказано, что это возможно только для
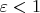
. Так что в принципе в магнитном поле тела левитировать могут несмотря на принцип максимума.



