В учебнике указано, что категория, все стрелки которой образуют множество, называется малой, и что все объекты малой категории тоже образуют множество. Верно ли обратное утверждение - что если все объекты категории образуют множество, то категория малая?
Если такое утверждение неверно, то есть ли общепринятый термин для категории, все объекты которой образуют множество?
Нет, неверно, контрпример есть на странице 216. Общепринятого названия нет, потому что пользы нет.
-- 13.04.2017, 19:53 --В примере 5.7 разве стрелки, соответствующие единичным морфизмам, не должны быть пунктирные?
Нет, не должны. Пунктирная стрелка означала бы "

- единственная стрелка такая, что

", а это не утверждается и может быть неверным (бывают, например, стрелки со свойством

).
-- 13.04.2017, 19:56 --Определение 6.1 - не очень понятно "что делать" если стрелки между
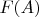
и

никакой нет.
Если нет стрелки, то нет и естественного преобразования. Далеко не между любыми функторами есть хоть одно естественное преобразование (как не между любыми объектами есть хоть один морфизм)
-- 13.04.2017, 20:07 --Цитата:
Подчёркиваю, единственное отличие от определения 1.1 в том, что
по протоморфизму его начало и конец не обязаны определяться одно-
значно.
В частности, может не быть начала/конца?
Да, вот это хороший вопрос. Посмотрел в книгу Фрейда-Щедрова, действительно, может не быть начала-конца! Но когда мы строим морфизмы в виде троек

, протоморфизмы без начала и конца исчезают за ненадобностью.
-- 13.04.2017, 20:12 --Как-то с самого начала возник вопрос, а что подразумевается под равенством стрелок?
Равенство стрелок - это просто равенство без всяких затей. Например, что понимается под равенством действительных чисел? Вот так же и со стрелками. Проблемы равенства нас на данном этапе не волнуют.
Хорошо, что стали спрашивать. Спрашивайте, я отвечаю.