У меня 2 вопроса, кот.не описаны в учебниках так подробно, как мне нужно.
1. Как читается запись функции:

? Т.к. ф-ция

определена на мн-ве всех

, то я читаю "эф на икс".
2. В учебнике читаю: " Нетрудно заметить, что ордината ф-ции

в точке

равна ординате графика функции

в точке

".
Я начинаю рассуждать и прихожу к выводу, что

может принимать те же значения, что и

, и тогда выходит, что графики этих функций идентичны!?
Но это скорее всего неверно, т.к. далее написано: "Это значит, что график функции

может быть получен из графика функции

преобразованием симметрии относительно оси

".
Из этого я делаю вывод: Если

, то графики функций

,
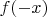
,

будут различаться только ординатой (выражением после знака равно в

), а их абсциссы будут равны?!



