Люди, порой, не видят очевидные вещи [нелин. аппроксимация]

[prof.uskov]

Евгений Машеров в сообщении #1159370 писал(а):

Вообще, нелинейное преобразование делается в трёх видах:
1. Линеаризация модели по параметрам.
2. Стабилизация дисперсии.
3. Приближение распределения к нормальному (нормализация, но тут надо иметь в виду, что иногда этим термином обозначают приведение случайной величины к нулевому матожиданию и единичной дисперсии, то есть линейное преобразование).
Эти цели различны и могут быть противоречивы (не всегда, но если согласуются - это большая удача; как z-преобразование Фишера $z=\ln\frac{1+r} {1-r}$ или его же арксинус-преобразование долей $\varphi=\arcsin\sqrt {p}$ - и то, и то стабилизирует дисперсию и приближает распределение к нормальному).

Стабилизация дисперсии - имеете в виду взвешенный МНК?
Приближение распределения к нормальному - это как?

[Евгений Машеров]

prof.uskov в сообщении #1159375 писал(а):

Стабилизация дисперсии - имеете в виду взвешенный МНК?

Нет. Взвешивание - это совершенно иной инструмент для этой же задачи.

[prof.uskov]

Евгений Машеров в сообщении #1159385 писал(а):

prof.uskov в сообщении #1159375 писал(а):

Стабилизация дисперсии - имеете в виду взвешенный МНК?

Нет. Взвешивание - это совершенно иной инструмент для этой же задачи.

Литературу не подскажете?

[dsge]

prof.uskov в сообщении #1159220 писал(а):

МНК оценка оптимальна лишь при выполнении целого ряда условий, которые на практике или выполняются с натягом, или вообще не выполняются. Например, если распределение аддитивной помехи имеет тяжелые хвосты, то более эффективной будет оценка минимума абсолютных отклонений, а не МНК.

Это неправда. МНК будет эффективной оценкой в классе линейных моделей, независимо от вида распределения случайного члена.

[--mS--]

dsge в сообщении #1159427 писал(а):

Это неправда. МНК будет эффективной оценкой в классе линейных моделей, независимо от вида распределения случайного члена.

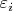
Как это? Скажем, для $X_i=\mu+\varepsilon_i$, $i=1,\ldots,n$, если $\varepsilon_i$ имеют распределение Лапласа с нулевым средним и дисперсией $2$, МНК-оценка для $\mu$ есть выборочное среднее, а ОМП-оценка - выборочная медиана.

И (если верить, например, вот этим выкладкам http://file.scirp.org/Html/6-1240248_41538.htm - а оснований не верить нет), то, скажем, для $n=3$ дисперсия выборочной медианы есть $0,95833$ от дисперсии среднего. Так что ОМНК в этом случае никак не эффективна.

Наверное, Вы хотели сказать, что ОМНК будет эффективной среди линейных оценок, а не линейных моделей регрессии, но это абсолютно разные вещи.

[prof.uskov]

dsge в сообщении #1159427 писал(а):

prof.uskov в сообщении #1159220 писал(а):

МНК оценка оптимальна лишь при выполнении целого ряда условий, которые на практике или выполняются с натягом, или вообще не выполняются. Например, если распределение аддитивной помехи имеет тяжелые хвосты, то более эффективной будет оценка минимума абсолютных отклонений, а не МНК.

Это неправда. МНК будет эффективной оценкой в классе линейных моделей, независимо от вида распределения случайного члена.

См. Демиденко "Линейная и нелинейная регрессия" стр. 172-186. Там все объяснено и даже результаты численного моделирования приведены из западных публикаций. Оценка МНК эффективна (имеет минимальную дисперсию) лишь только для ограниченного класса распределений, в том числе и для нормального распределения http://www.twirpx.com/file/244620/

[dsge]

--mS-- в сообщении #1159478 писал(а):

Наверное, Вы хотели сказать, что ОМНК будет эффективной среди линейных оценок, а не линейных моделей регрессии, но это абсолютно разные вещи.

Конечно оценок.

prof.uskov в сообщении #1159547 писал(а):

См. Демиденко "Линейная и нелинейная регрессия" стр. 172-186. Там все объяснено и даже результаты численного моделирования приведены из западных публикаций. Оценка МНК эффективна (имеет минимальную дисперсию) лишь только для ограниченного класса распределений, в том числе и для нормального распределения http://www.twirpx.com/file/244620/

У Демиденко речь идет, про совсем другое, про выбросы, которые не имеют распределений, а не про распределение ошибок. Сравнивается неэффективность предлагаемых методов по сравнению с МНК в случае отсутствия выбросов и "выигрыш" в случае их присутствия.
Повторю ещё раз МНК эффективная оценка для любого распределения ошибок в классе линейных оценок.

[prof.uskov]

dsge в сообщении #1159563 писал(а):

--mS-- в сообщении #1159478 писал(а):

Наверное, Вы хотели сказать, что ОМНК будет эффективной среди линейных оценок, а не линейных моделей регрессии, но это абсолютно разные вещи.

Конечно оценок.

prof.uskov в сообщении #1159547 писал(а):

См. Демиденко "Линейная и нелинейная регрессия" стр. 172-186. Там все объяснено и даже результаты численного моделирования приведены из западных публикаций. Оценка МНК эффективна (имеет минимальную дисперсию) лишь только для ограниченного класса распределений, в том числе и для нормального распределения http://www.twirpx.com/file/244620/

У Демиденко речь идет, про совсем другое, про выбросы, которые не имеют распределений, а не про распределение ошибок. Сравнивается неэффективность предлагаемых методов по сравнению с МНК в случае отсутствия выбросов и "выигрыш" в случае их присутствия.

Вы точно посмотрели?
Стр. 183 вверху: "...Сравнение начнем с исследования свойств Lv-оценок. В [176] исследована эффективность оценки... и разных распределений отклонений...
... Для распределения с конечной дисперсией и легкими хвостами (типа нормального) наиболее эффективной будет оценка МНК... Для распределений с тяжелыми хвостами... "

[dsge]

Если минимизировать не квадратичные, а с другой степенью отклонения, т.е. те, которые рассмотрены в книге, то такие оценки уже не будут линейными.

[prof.uskov]

dsge в сообщении #1159576 писал(а):

Если минимизировать не квадратичные, а с другой степенью отклонения, т.е. те, которые рассмотрены в книге, то такие оценки уже не будут линейными.

А зачем нам линейные? Что она нам дает? Мы практические задачи решаем, а не теорией занимаемся.

[dsge]

На практике проще, быстрее, точнее считать; решение задачи оптимизации всегда единственно (это, правда, верно для любой выпуклой целевой функции, однако, минимум может оказаться негладким или очень "плоским"). В случае нормальности ошибок оценки будут нормальными, значит можно гипотезы тестировать.

[prof.uskov]

dsge в сообщении #1159584 писал(а):

На практике проще, быстрее, точнее считать; решение задачи оптимизации всегда единственно. В случае нормальности ошибок оценки будут нормальными, значит можно гипотезы тестировать.

На счет быстрее считать и лучше оптимизировать при современной вычислительной технике неактуально.
На счет проверять гипотезы, это да. Но цель-то в получении хороших моделей, а не красивого математического обоснования.
Исследователь сам не выбирает ошибку, какая досталась, с такой и работает, иметь нормальную - большое везение.

[dsge]

prof.uskov в сообщении #1159587 писал(а):

Но цель-то в получении хороших моделей, а не красивого математического обоснования.

Какой критерий "хорошести" модели?

prof.uskov в сообщении #1159587 писал(а):

На счет быстрее считать и лучше оптимизировать при современной вычислительной технике неактуально.

Даже при современной вычислительной технике имеются некоторые проблемы с задачами с неединственным решением.

-- 13.10.2016, 20:59 --

prof.uskov в сообщении #1159587 писал(а):

Исследователь сам не выбирает ошибку, какая досталась, с такой и работает, иметь нормальную - большое везение.

Обычная практика - это сначала попытаться использовать классический инструментарий - линейная модель, МНК, предположение о нормальности и т.п., протестировать обоснованность этих предположений, если всё отвергается, то искать что-то другое.

[prof.uskov]

dsge в сообщении #1159589 писал(а):

prof.uskov в сообщении #1159587 писал(а):

Но цель-то в получении хороших моделей, а не красивого математического обоснования.

Какой критерий "хорошести" модели?

Давайте еще раз все уточним. Выполняются предпосылки регрессионного анализа. Имеем линейную (линейную по параметрам или нелинейную) модель, в которой необходимо определить коэффициенты, таким образом, чтобы остаточная дисперсия была минимальной. Эффективная оценка имеет наименьшую дисперсию.
Если аддитивная помеха нормально распределена, то наименьшую дисперсию обеспечивает МНК.
Если помеха имеет тяжелые хвосты, то МНК уже не эффективен, нужна более медленная функция для определения расстояния, чем квадрат. Для "узких распределений" наоборот более эффективный метод определения расстояния с большей степенью чем квадрат.

[madschumacher]

(Оффтоп)

prof.uskov в сообщении #1159587 писал(а):

На счет быстрее считать и лучше оптимизировать при современной вычислительной технике неактуально.

ну-ну... учитывая, что иногда в прикладных задачах оптимизации стоит задача тупо "распределить" данные по памяти компьютера (а даже не скорости их обработки )... Да ещё и задачи сами нелинейные, а ещё они могут быть некорректно поставленными (с этим ещё мучиться), а может быть, что формально поставлена корректно, но численно -- нестабильная... Так что, да, конечно, неактуально.