Универсального алгоритма для конечных сумм и рядов произвольного вида, как я понимаю, нет.
Это так странно, учитывая, что для неопределенных интегралов
он существует.
Между прочим, хорошая мысль! Действительно, почему бы не попробовать свести одну задачу к другой. Пусть у нас есть бесконечный ряд
, в общем случае не обязательно сходящийся. Требуется найти замкнутую формулу для суммы
.
Обозначим
. Здесь
можно назвать
-й частичной суммой ряда. Почему именно
-й? Потому что в данную сумму входит ровно
первых членов ряда. Я знаю, в большинстве случаев принято искать общую формулу вот для такой суммы:
, в которую входит
член, от
до
. В некоторых случаях это действительно удобно, и о них мы поговорим позже. Но на самом деле это не принципиально: если найдена замкнутая формула для
членов, нетрудно по ней построить аналогичную формулу и для
членов. И наоборот.
Далее нужно обратить внимание на следующее: очевидно, что
. Такое уравнение называется линейным неоднородным разностным уравнением первого порядка. Про такие уравнения известно, что в "однородном" случае (когда правая часть нулевая) они решаются легко и просто. Потому что существует метод их решения. Про неоднородные же уравнения можно сказать, что общее решение неоднородного уравнения получается как сумма общего решения однородного уравнения и какого-либо частного решения неоднородного уравнения. Однако же общих способов определения частного решения не существует (или не известно)! И это понятно: если бы они существовали, существовал бы и алгоритм по свертыванию частичных сумм в замкнутые формулы, типа того, который существует для интегралов. Тем не менее, для некоторых специальных видов функции в правой части уравнения существуют стандартные приемы решения этого уравнения. Например, всем известный телескопический ряд
, который легко "раскладывается" на две "половины":
. Здесь сразу же очевидно, что
. Т.е. решение сразу готово.
Кстати, глядя на разностное уравнение
можно подумать, что функция
может быть найдена с точностью до константы. Т.е. если
является решением уравнения, то и
также будет решением, где
- некоторая константа. На самом деле, это не так! Ведь мы уже договорились, что
означает сумму
первых членов ряда. В таком случае сумма нуля членов должна равняться нулю, т.е. должно быть верным
. Кажется, что не всегда это возможно, например, не в случае
. На самом деле, дело в том, что решение было найдено не верно! Правильное решение выглядит так:
.
Ок, если общих методов не существует, значит, остается только перебрать все возможные типы специальных функций и посмотреть, к какому из них относится наша функция. Затем применить к ней соответствующий прием и записать решение. Либо констатировать, что решения нет (в элементарных функциях), если ни к какому не относится. Наверняка, автоматизированные сервисы именно так и работают. Быть может, однако, здесь можно придумать что-то еще...
1)
Преобразование ФурьеНайдем преобразование Фурье для обеих частей нашего разностного уравнения!
Применяя преобразование, получим
.
Здесь большими буквами обозначены фурье-образы для функций, обозначенных соответствующими маленькими буквами.
Решаем это уравнение и получаем
.
Ну, и всё. Осталось сделать только обратное преобразование. Обратное преобразование - всегда некоторый интеграл. Если он выражается в элементарных функциях, значит, и функция
тоже в них выражается. Главное только при решении интеграла не получить исходный ряд. Как говорится, в расследовании главное не выйти на самого себя :)
Можно также оставить этот интеграл, как есть, считая его самого "замкнутой формой".
На самом деле, основная проблема здесь заключается в том, что для большинства функций преобразование Фурье попросту не существует. Оно существует только для нескольких специальных видов функций.
Можно ли то же самое проделать с уравнением, применяя преобразование Лапласа? Здесь я бы уже не был так уверен. Дело в том, что преобразование Лапласа применяется к функциям, равным нулю в отрицательной области. Казалось бы, это не имеет особого значения, поскольку сам интеграл преобразования берется в промежутке от нуля до бесконечности, так что какая разница? Дело в том, однако, что функция
получена сдвигом функции
на единицу влево. Значит, у нее появились ненулевые значения в отрицательной области. Если мы затем начнем ее интегрировать от нуля до бесконечности, не потеряем ли мы часть значений? Это ведь совсем не то же самое, что сдвинуть функцию
вправо. Потому что в этом случае ее значения на отрезке
![$[0;1]$](https://dxdy-03.korotkov.co.uk/f/2/1/a/21ad730ee7df0b97abd700cb0f8426e682.png "$[0;1]$")
станут равны нулю, и в этом случае действительно уже всё равно, от какого значения ее интегрировать: от 0 или от 1.
Короче, я бы в данном случае перестраховался и искал преобразование для какого-нибудь такого уравнения:
. Затем, если решение будет найдено, тогда функцию
можно было бы получить из тождества
.
2)
Интегральное уравнениеМожно действовать и более прямолинейно. Представим, что в уравнении
функция
является первообразной для некоторой функции
. В таком случае уравнение можно переписать так:
![$\[f(x) = \int\limits_x^{x + 1} {h(t)dt} \]$](https://dxdy-01.korotkov.co.uk/f/4/a/0/4a06dc77a544dfb4eb2e9c4802f9e02082.png "$\[f(x) = \int\limits_x^{x + 1} {h(t)dt} \]$")
.
Получилось интегральное уравнение относительно неизвестной функции
с известной функцией
. Понятно, что если решение этого уравнения существует в элементарных функциях, то... а хотя, нет. Если
- элементарная функция, то ее первообразная - вовсе не обязательно. Тем не менее, ясно, что было бы полезно решить такое уравнение.
Для этого я перепишу уравнение так:
![$\[f(x) = \int\limits_0^\infty {K(x,t)h(t)dt} \]$](https://dxdy-04.korotkov.co.uk/f/7/0/2/7021a5a2d67538a93212766e9e99ab7282.png "$\[f(x) = \int\limits_0^\infty {K(x,t)h(t)dt} \]$")
Здесь функция
равна единице, когда
![$\[x \le t \le x + 1\]$](https://dxdy-03.korotkov.co.uk/f/a/0/7/a075ab5b88d84dc787f05459f1bb626c82.png "$\[x \le t \le x + 1\]$")
, и нулю во всех остальных случаях.
Такая форма будет эквивалентной хотя бы для положительных значений
, а только такие, на самом деле, нас и интересуют. Можно получить и общую форму, верную и для отрицательных значений
. Для этого всего лишь нужно поменять нижний предел интеграла с нуля на минус бесконечность. Однако я все-таки остановлюсь на нуле, поскольку дальше этот интеграл будем рассматривать, как свертку двух функций, от которой можно взять преобразование Лапласа. А свертка для преобразования Лапласа формулируется именно в виде интеграла от 0 до бесконечности. Хотя, я не знаю, почему это именно так: на мой взгляд, если сформулировать ее от минус бесконечности до бесконечности, ошибки не произойдет - особенно если считать, что все функции равны нулю в отрицательной области (кроме, конечно,
). В случае с преобразованиями Фурье именно так и делают. Но да бог с ним: сформулирую, как принято, чтобы не отклоняться от правил и не наделать ошибок.
Полученное уравнение называют неоднородным уравнением Фредгольма первого рода, функция
называется ядром этого уравнения. Полученное уравнение можно решить с помощью преобразования Лапласа, если удастся свести функцию
к некоторой функции
одного аргумента, потому что в этом случае интеграл этого уравнения станет сверткой двух функций,
и
. А преобразование Лапласа от свертки равно произведению лаплас-образов каждой из двух функций
и
по отдельности. Поэтому именно это я дальше и попытаюсь сделать.
Функцию
лучше всего будет представить в виде разности двух единичных ступенчатых функций – функций Хевисайда
.
Во-первых, потому что нужна единая формула для
для всех возможных случаев (а не так, что здесь 1, там 0, и т.д.).
Во-вторых, потому что нужна функция одного аргумента, на место которого можно будет подставить
, чтобы получилась свертка.
В-третьих, потому что преобразование Лапласа хорошо берется от ступенчатой функции.
Итак,
![$\[K(x,t) = \theta (x + 1 - t) - \theta (x - t) = q(x - t)\]$](https://dxdy-02.korotkov.co.uk/f/d/9/9/d992cc2133969a79b81a86366481776a82.png "$\[K(x,t) = \theta (x + 1 - t) - \theta (x - t) = q(x - t)\]$")
, где
![$\[q(x) = \theta (x + 1) - \theta (x)\]$](https://dxdy-03.korotkov.co.uk/f/2/7/1/271cad58a63cd9951df77d0b96a182b882.png "$\[q(x) = \theta (x + 1) - \theta (x)\]$")
.
Тогда интегральное уравнение можно переписать так:
![$\[f(x) = \int\limits_0^\infty {q(x - t)h(t)dt} \]$](https://dxdy-03.korotkov.co.uk/f/a/4/7/a47e5071a889a25dc588ad5bde12556e82.png "$\[f(x) = \int\limits_0^\infty {q(x - t)h(t)dt} \]$")
.
Дальше, как можно догадаться, берем преобразование Лапласа от обеих частей уравнения.
Обозначим:
- образ функции
- образ функции
- образ функции
При этом
![$\[Q(s) = {e^s}/s - 1/s = ({e^s} - 1)/s\]$](https://dxdy-04.korotkov.co.uk/f/b/5/f/b5f256a50517fd59036aeb0ea587b67082.png "$\[Q(s) = {e^s}/s - 1/s = ({e^s} - 1)/s\]$")
.
Тогда получаем уравнение
![$F(s)=Q(s)H(s)=H(s)\[({e^s} - 1)/s\]$](https://dxdy-04.korotkov.co.uk/f/b/4/a/b4a414bf8c0da4bb4b987f79e687b09582.png "$F(s)=Q(s)H(s)=H(s)\[({e^s} - 1)/s\]$")
, решая которое, получаем
![$\[H(s) = sF(s)/({e^s} - 1)\]$](https://dxdy-01.korotkov.co.uk/f/8/d/d/8dd9d25e199fff133855f6c329f1826282.png "$\[H(s) = sF(s)/({e^s} - 1)\]$")
.
На самом деле, этот же результат можно было получить намного короче, если вспомнить, что для случая, когда
является первообразной для
, верно
. А получать
мы уже умеем - это было описано в предыдущем пункте.
Самое интересное - что теперь со всем этим делать. Оригинал для
нам известен - это
. Остается получить оригинал для
![$\[s/({e^s} - 1)\]$](https://dxdy-03.korotkov.co.uk/f/2/d/5/2d57ce71981f6325403407574b8bbaa082.png "$\[s/({e^s} - 1)\]$")
, составить свертку для этих двух функций - это и будет "замкнутая форма" для
. Проблема в том, что оригинал для
(как и для
![$\[1/({e^s} - 1)\]$](https://dxdy-01.korotkov.co.uk/f/c/5/d/c5df0fb2bc258d25cbc05d838c4d681c82.png "$\[1/({e^s} - 1)\]$")
) не существует в элементарных функциях. Для
это будет, скорее всего, бесконечная сумма дельта-функций Дирака с разной степенью сдвига. Для
- что-нибудь и того хуже.
Но я предлагаю не заморачиваться слишком сильно, а сразу брать свою функцию
и идти с ней куда-нибудь на сервис
www.wolframalpha.com. Там применить к ней преобразование Лапласа (Laplace transform). Если получилось что-то осмысленное, умножить на
или на
, а затем применить обратное преобразование Лапласа (inverse Laplace transform). Если опять получился результат в элементарных функциях, значит, метод сработал.
3)
Метод операторовУравнение
можно переписать в виде
![$\[\Delta g(n) = f(n)\]$](https://dxdy-04.korotkov.co.uk/f/7/0/3/70318ffbe42f7673f0a2eb03ac4acbc882.png "$\[\Delta g(n) = f(n)\]$")
. Здесь
- оператор, означающий взятие от функции ее первой конечной разности:
![$\[\Delta f(n) = f(n + 1) - f(n)\]$](https://dxdy-04.korotkov.co.uk/f/f/0/9/f092b8d62b8495d0ea87d439118fc28282.png "$\[\Delta f(n) = f(n + 1) - f(n)\]$")
. Этот оператор можно представить в виде
![$\[\Delta = E - 1\]$](https://dxdy-04.korotkov.co.uk/f/f/5/8/f58c1b4f9fadcc4c9c00fcc49fe1b3ea82.png "$\[\Delta = E - 1\]$")
, где
- оператор сдвига (т.е. такой, что
),
- тождественный оператор, т.е. такой, что ставит функцию в соответствие самой себе:
.
Тогда наше уравнение принимает вид
. Решая его, получаем:
![$\[g(n) = f(n)/(E - 1) = - (1/(1 - E))f(n) = - (1 + E + {E^2} + {E^3} + ...)f(n) = - \sum\limits_{k = 0}^\infty {f(n + k)} \]$](https://dxdy-01.korotkov.co.uk/f/0/e/3/0e3697f3bc6d8be34f24545d9d98598782.png "$\[g(n) = f(n)/(E - 1) = - (1/(1 - E))f(n) = - (1 + E + {E^2} + {E^3} + ...)f(n) = - \sum\limits_{k = 0}^\infty {f(n + k)} \]$")
Получился совершенно точный, но при этом абсолютно бесполезный результат.
Подробнее об элементарной теории операторов можно почитать в книжке Грэхема и Кнута "Конкретная математика" (глава 5: специальные приемы).
4)
Производящая функция 
z-преобразованиеЭтот метод, пожалуй, единственный позволяет получить какие-то конкретные результаты на практике.
Пусть есть последовательность
, где
.
Производящей функцией такой последовательности называется функция
такая, что
![$\[A(x) = \sum\limits_{k = 0}^\infty {{a_k}{x^k}} \]$](https://dxdy-01.korotkov.co.uk/f/0/7/a/07a3142141a3fc1390e9e87c3b16b02a82.png "$\[A(x) = \sum\limits_{k = 0}^\infty {{a_k}{x^k}} \]$")
.
При этом сама последовательность
может быть задана какой-нибудь функцией
:
.
Метод начинается с того, что надо как-то получить замкнутую форму для функции
. И здесь даже не надо строить иллюзий: никаких общих методов это сделать нет! Возможно, эта задача даже сложнее, чем получить замкнутую формулу для частичной суммы. За исключением некоторых случаев, например, для последовательности
получить замкнутую формулу в элементарных функциях в принципе невозможно (сейчас это будет доказано), тогда как производящей функцией этой последовательности является самая обычная экспонента.
Собственно, я даже догадываюсь, с чем связано это затруднение. Получение производящей функции по последовательности - это задача, обратная задаче разложения функции в ряд Тейлора. А обратные задачи в большинстве случаев решаются почему-то труднее прямых. Сравнить, например, интегрирование с дифференцированием. Существует общий метод получить производную ЛЮБОЙ элементарной функции. И даже иногда, если она не элементарная. Однако интеграл от элементарной функции - не всегда элементарная функция.
Кстати, не один я так считаю. Например, Иванов Б. Н. в своей книге "Дискретная математика. Алгоритмы и программы", в
главе 3 пишет, что как правило, поиск производящей функции по определению прямыми методами является сложной задачей. Однако заметим, что сама последовательность может быть восстановлена по производящей функции (т.е. обратная задача решается хорошо - мое прим.).
Ничего удивительного, кстати говоря. Как только функция A(x) получена, мы сразу же можем вычислить сумму бесконечного ряда, просто подставив x=1 в A(x) (конечно, если функция A(x) существует в этой точке). Однако в общем случае вычисление бесконечных рядов - задача нетривиальная.
Метод производящей функции, однако, обладает той интересной особенностью, что нет необходимости следить за сходимостью полученного ряда, поскольку символ
в разложении не означает какого-то числа, которое можно было бы подставить на его место. Это просто формальный символ. И тем не менее, метод позволяет получать какие-то содержательные результаты, верность которых затем можно проверять, например, по индукции. Однако прежде чем проверить какой-то результат, его требуется откуда-то получить. Вот это и есть такой метод.
Короче, начинаем с того, что замкнутая форма для
у нас откуда-то уже имеется, на этом не останавливаемся. Тогда коэффициент при
в разложении функции
в ряд Тейлора будет равен
![$\[\sum\limits_{k = 0}^n {{a_k}} \]$](https://dxdy-04.korotkov.co.uk/f/7/c/9/7c9c61270a013931ffa6db7cdd7cfe9a82.png "$\[\sum\limits_{k = 0}^n {{a_k}} \]$")
. Вот здесь как раз возникает случай, когда суммируется
членов ряда, от
до
.
На доказательстве этого факта я не останавливаюсь. Можно воспользоваться
методом производящего ряда, где для рекуррентной формулы получают соответствующее уравнение в производящих функциях. Получится уравнение, похожее на уравнение для фурье-образов из первого пункта, типа такого:
. Можно использовать свертку двух последовательностей, одну из которых задать, как {
}. Про свертку последовательностей можно почитать в википедии, в статье "Производящая функция последовательности". Само доказательство есть в книге Грэхема и Кнута "Конкретная математика", в главе 7 "Производящие функции". В разделе "Основные маневры" говорится, что "умножение производящей функции на
дает производящую функцию для последовательности частичных сумм исходной посдедовательности". При этом под частичной суммой, очевидно, у них понимается сумма
начальных членов.
Короче, вся соль теперь в том, как найти замкнутую форму для коэффициента при
в разложении
в ряд Тейлора. В этом может помочь
z-преобразование.
По определению, z-преобразование последовательности функций {
}, это функция
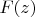
такая, что
. z-преобразование существует не для всех видов функций, а только для тех, что растут не быстрее экспоненты, но не суть.
Таким образом, очевидно, что z-преобразование применяется не к одной конкретной функции, а сразу ко всей последовательности. При этом смысл этого преобразования в том, что по функции
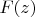
можно получить произвольный член последовательности {
} по формуле
![$$\[f(k) = \frac{1}{{2\pi i}}\oint\limits_C {F(z){z^{k - 1}}dz} \]$$](https://dxdy-03.korotkov.co.uk/f/2/3/e/23eb940ba2fef5c8d60f4b94f774c5c282.png "$$\[f(k) = \frac{1}{{2\pi i}}\oint\limits_C {F(z){z^{k - 1}}dz} \]$$")
. Интеграл берется по любому замкнутому контуру, включающему все особые точки
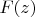
. Спрашивается, зачем нужна функция
, если она и так уже имеется по условию? Ни зачем она не нужна! Нужен член последовательности частичных сумм. А это значит, что надо найти z-преобразование вот для такой производящей функции:
. А затем применить к нему обратное z-преобразование.
Как видно, поиск частичной суммы ряда опять свелся к некоторому интегралу, пусть и комплексному. Но это не так уж и страшно, как сейчас станет ясно.
Обозначим {
} последовательность частичных сумм исходной последовательности {
}. Здесь
, где
. Как видно, здесь придется отойти от первоначального определения функции
, как суммы
первых членов рядов, и складывать уже
начальный член.
Производящей функцией последовательности {
} обозначим
, где
. Ну а z-преобразование для
обозначим, как
.
Тогда
![$\[G(z) = B(1/z) = \frac{{A(1/z)}}{{1 - 1/z}} = \frac{{F(z)}}{{1 - 1/z}} = \frac{{zF(z)}}{{z - 1}}\]$](https://dxdy-04.korotkov.co.uk/f/3/c/8/3c8dea15be2d0f3e674d0fa384bc6d5f82.png "$\[G(z) = B(1/z) = \frac{{A(1/z)}}{{1 - 1/z}} = \frac{{F(z)}}{{1 - 1/z}} = \frac{{zF(z)}}{{z - 1}}\]$")
,
откуда получаем
![$$\[g(k) = \frac{1}{{2\pi i}}\oint\limits_C {G(z){z^{k - 1}}dz} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{zF(z)}}{{z - 1}}{z^{k - 1}}dz} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{{z^k}F(z)}}{{z - 1}}dz} \]$$](https://dxdy-04.korotkov.co.uk/f/7/d/a/7daa0768b73a61940541d831c8a1ef0282.png "$$\[g(k) = \frac{1}{{2\pi i}}\oint\limits_C {G(z){z^{k - 1}}dz} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{zF(z)}}{{z - 1}}{z^{k - 1}}dz} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{{z^k}F(z)}}{{z - 1}}dz} \]$$")
.
Рассмотрим какой-нибудь пример.
можно найти замкнутое выражение для суммы вида 
(см. у Кнута по ссылке выше). Есть и другие "вычислимые" классы сумм. Некоторые ряды удаётся суммировать средствами операционного исчисления (хотя Вы, вероятно, об этом знаете).
Ну, хотя бы про 
-ние операционного исчисления мне известно, уже хорошо. 
. Тогда можно написать
, нужно найти 
при начальном условии 
.
. Покажем, что она представляет значение искомой суммы. Для этого заметим, что при 
выполнено
действительно равна значению искомой суммы:
. Имеем
. Таким образом, нам нужно найти частичную сумму 
.
, по легенде впервые полученная Карлом Гауссом, когда он еще учился в школе. Она-то и будет для нас ориентиром при проверке решения. ![$\[A(x) = \sum\limits_{k = 0}^\infty {k{x^k}} = x\sum\limits_{k = 0}^\infty {k{x^{k - 1}}} = x\sum\limits_{k = 0}^\infty {({x^k})'} = x\left( {\sum\limits_{k = 0}^\infty {{x^k}} } \right)' = x\left( {\frac{1}{{1 - x}}} \right)' = \frac{x}{{{{(1 - x)}^2}}}\]$](https://dxdy-04.korotkov.co.uk/f/b/9/4/b946d03759a0369fbc365ecaabb6c57082.png "$\[A(x) = \sum\limits_{k = 0}^\infty {k{x^k}} = x\sum\limits_{k = 0}^\infty {k{x^{k - 1}}} = x\sum\limits_{k = 0}^\infty {({x^k})'} = x\left( {\sum\limits_{k = 0}^\infty {{x^k}} } \right)' = x\left( {\frac{1}{{1 - x}}} \right)' = \frac{x}{{{{(1 - x)}^2}}}\]$")
.![$\[G(z) = \frac{{zF(z)}}{{z - 1}} = \frac{{zA(z)}}{{z - 1}} = \frac{{{z^2}}}{{{{(z - 1)}^3}}}\]$](https://dxdy-03.korotkov.co.uk/f/e/c/e/eceb682dcf2ac720e9399728676887d482.png "$\[G(z) = \frac{{zF(z)}}{{z - 1}} = \frac{{zA(z)}}{{z - 1}} = \frac{{{z^2}}}{{{{(z - 1)}^3}}}\]$")
.![$\[\sum\limits_{k = 0}^n k = g(n) = \frac{1}{{2\pi i}}\oint\limits_C {G(z){z^{n - 1}}dz} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{{z^{n + 1}}}}{{{{(z - 1)}^3}}}dz} \]$](https://dxdy-02.korotkov.co.uk/f/5/f/7/5f726be717cbba2dac9b5b34ca7a7aa582.png "$\[\sum\limits_{k = 0}^n k = g(n) = \frac{1}{{2\pi i}}\oint\limits_C {G(z){z^{n - 1}}dz} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{{z^{n + 1}}}}{{{{(z - 1)}^3}}}dz} \]$")
.![$$\[w({z_0}) = \frac{1}{{2\pi i}}\oint\limits_L {\frac{{w(z)}}{{z - {z_0}}}dz} \]$$](https://dxdy-01.korotkov.co.uk/f/c/b/4/cb44d76c58b1d300354db93c60bd595082.png "$$\[w({z_0}) = \frac{1}{{2\pi i}}\oint\limits_L {\frac{{w(z)}}{{z - {z_0}}}dz} \]$$")
.
функция 
не существует, и мы ее там вычислить не сможем. Поэтому надо воспользоваться более изощренной версией этой формулы:![$$\[{w^{(m)}}({z_0}) = \frac{{m!}}{{2\pi i}}\oint\limits_L {\frac{{w(z)}}{{{{(z - {z_0})}^{m + 1}}}}dz} \]$$](https://dxdy-04.korotkov.co.uk/f/3/4/6/34651919fb4b6ee08fbba55921e5d17782.png "$$\[{w^{(m)}}({z_0}) = \frac{{m!}}{{2\pi i}}\oint\limits_L {\frac{{w(z)}}{{{{(z - {z_0})}^{m + 1}}}}dz} \]$$")
в знаменателе формулы получилась такой же, как и в нашем примере. Поскольку в нашем примере степень знаменателя равна тройке, нужно выбрать 
, чтобы 
. В таком случае, для нашего примера функция 
будет равна 
. И нужно затем продифференцировать ее 
. Я не знаю, насколько доступно я всё это объясняю. Тут нет ничего, кроме использования формулы Коши. Только сперва требуется выбрать из них всех наиболее подходящую (с подходящим значением для 
, получится 
. А такую функцию в точке ![$\[\sum\limits_{k = 0}^n k = g(n) = \frac{1}{{2\pi i}}\oint\limits_L {\frac{{{z^{n + 1}}}}{{{{(z - 1)}^3}}}dz} = {\left. {\left( {\frac{{({z^{n + 1}})''}}{{2!}}} \right)} \right|_{z = 1}} = \frac{{(n + 1)n{1^{n - 1}}}}{{2!}} = \frac{{(n + 1)n}}{2}\]$](https://dxdy-04.korotkov.co.uk/f/b/f/9/bf9ea9e9099db8db1b48273c6b58140982.png "$\[\sum\limits_{k = 0}^n k = g(n) = \frac{1}{{2\pi i}}\oint\limits_L {\frac{{{z^{n + 1}}}}{{{{(z - 1)}^3}}}dz} = {\left. {\left( {\frac{{({z^{n + 1}})''}}{{2!}}} \right)} \right|_{z = 1}} = \frac{{(n + 1)n{1^{n - 1}}}}{{2!}} = \frac{{(n + 1)n}}{2}\]$")
.![$\[\frac{{{A^{(n)}}(0)}}{{n!}} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{A(u)}}{{{u^{n + 1}}}}du} = [u = 1/z] = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{F(z)}}{{{{(1/z)}^{n + 1}}}}\frac{{ - 1}}{{{z^2}}}dz} = - \frac{1}{{2\pi i}}\oint\limits_C {F(z){z^{n - 1}}dz} \]$](https://dxdy-04.korotkov.co.uk/f/b/8/6/b86308cd762ce07eca4070ca43d1575482.png "$\[\frac{{{A^{(n)}}(0)}}{{n!}} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{A(u)}}{{{u^{n + 1}}}}du} = [u = 1/z] = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{F(z)}}{{{{(1/z)}^{n + 1}}}}\frac{{ - 1}}{{{z^2}}}dz} = - \frac{1}{{2\pi i}}\oint\limits_C {F(z){z^{n - 1}}dz} \]$")
. 
, 
,![$\[G(z) = \frac{{zF(z)}}{{z - 1}} = \frac{{z{e^{1/z}}}}{{z - 1}}\]$](https://dxdy-01.korotkov.co.uk/f/8/3/6/836012f9808063213abab3f98a119a4082.png "$\[G(z) = \frac{{zF(z)}}{{z - 1}} = \frac{{z{e^{1/z}}}}{{z - 1}}\]$")
.![$\[\sum\limits_{k = 0}^n {\frac{1}{{k!}}} = g(n) = \frac{1}{{2\pi i}}\oint\limits_C {G(z){z^{n - 1}}dz} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{{z^n}{e^{1/z}}}}{{z - 1}}dz} \]$](https://dxdy-04.korotkov.co.uk/f/3/2/6/326fa46fd855a0895a64d51b3646d07882.png "$\[\sum\limits_{k = 0}^n {\frac{1}{{k!}}} = g(n) = \frac{1}{{2\pi i}}\oint\limits_C {G(z){z^{n - 1}}dz} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{{z^n}{e^{1/z}}}}{{z - 1}}dz} \]$")
.
(т.е. числу Эйлера или основанию натурального логарифма). Уже понятно, что такой результат ошибочен: числу ![$\[\sum\limits_{k = 0}^\infty {\frac{1}{{k!}}} \]$](https://dxdy-02.korotkov.co.uk/f/1/5/3/153aed7fc879bafa8a56c89fe0120b8782.png "$\[\sum\limits_{k = 0}^\infty {\frac{1}{{k!}}} \]$")
. Но нам-то нужна частичная сумма такого ряда. Интересно, где же здесь ошибка? Вероятно, функция 
не удовлетворяет каким-то условиям этой теоремы. В любом случае, придется считать этот интеграл какими-то другими методами.![$\[z = r{e^{i\varphi }}\]$](https://dxdy-02.korotkov.co.uk/f/1/9/1/1916a902f3b1ef5cf8b2ab2ad1be335b82.png "$\[z = r{e^{i\varphi }}\]$")
. В этом случае комплексная экспонента как бы задает ту окружность радиуса 
, по которой будет взят интеграл. Но сам интеграл при этом приобретает уже обычный "римановский" вид:![$\[\sum\limits_{k = 0}^n {\frac{1}{{k!}}} = g(n) = \frac{1}{{2\pi i}}\oint\limits_C {G(z){z^{n - 1}}dz} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{{z^n}{e^{1/z}}}}{{z - 1}}dz} = [z = r{e^{i\varphi }}] = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{{e^{1/(r{e^{i\varphi }})}}}}{{r{e^{i\varphi }} - 1}}{{(r{e^{i\varphi }})}^n}d(r{e^{i\varphi }})} = \frac{{{r^n}}}{\pi }\int\limits_{ - \pi }^\pi {\frac{{{e^{1/(r{e^{i\varphi }})}}}}{{r{e^{i\varphi }} - 1}}{e^{i\varphi (n + 1)}}d\varphi } \]$](https://dxdy-04.korotkov.co.uk/f/7/0/a/70a5e245303b1ea025c3ea9d2f3e939382.png "$\[\sum\limits_{k = 0}^n {\frac{1}{{k!}}} = g(n) = \frac{1}{{2\pi i}}\oint\limits_C {G(z){z^{n - 1}}dz} = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{{z^n}{e^{1/z}}}}{{z - 1}}dz} = [z = r{e^{i\varphi }}] = \frac{1}{{2\pi i}}\oint\limits_C {\frac{{{e^{1/(r{e^{i\varphi }})}}}}{{r{e^{i\varphi }} - 1}}{{(r{e^{i\varphi }})}^n}d(r{e^{i\varphi }})} = \frac{{{r^n}}}{\pi }\int\limits_{ - \pi }^\pi {\frac{{{e^{1/(r{e^{i\varphi }})}}}}{{r{e^{i\varphi }} - 1}}{e^{i\varphi (n + 1)}}d\varphi } \]$")
.
. В данном случае особыми являются точки 
и 
, потому что в них функция 
- этого вполне должно хватить. И теперь идем на сервис Wolfram Alpha, чтобы 
. И действительно, ![$\[\sum\limits_{k = 0}^4 {\frac{1}{{k!}}} = \frac{1}{{0!}} + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} + \frac{1}{{4!}} = 1 + 1 + \frac{1}{2} + \frac{1}{6} + \frac{1}{{24}} = \frac{{24}}{{24}} + \frac{{24}}{{24}} + \frac{{12}}{{24}} + \frac{4}{{24}} + \frac{1}{{24}} = \frac{{65}}{{24}}\]$](https://dxdy-04.korotkov.co.uk/f/3/c/4/3c406b429f605fcfe10e198ed180563f82.png "$\[\sum\limits_{k = 0}^4 {\frac{1}{{k!}}} = \frac{1}{{0!}} + \frac{1}{{1!}} + \frac{1}{{2!}} + \frac{1}{{3!}} + \frac{1}{{4!}} = 1 + 1 + \frac{1}{2} + \frac{1}{6} + \frac{1}{{24}} = \frac{{24}}{{24}} + \frac{{24}}{{24}} + \frac{{12}}{{24}} + \frac{4}{{24}} + \frac{1}{{24}} = \frac{{65}}{{24}}\]$")
.![$\[\sum\limits_{k = 0}^n {\frac{1}{{k!}}} \]$](https://dxdy-03.korotkov.co.uk/f/2/a/0/2a0ebcc9edaab9cf373a8a25e758428982.png "$\[\sum\limits_{k = 0}^n {\frac{1}{{k!}}} \]$")
он считает вот ![$\[\sum\limits_{k = 0}^n {\frac{1}{{k!}}} = \frac{{e\Gamma (n + 1,1)}}{{\Gamma (n + 1)}}\]$](https://dxdy-03.korotkov.co.uk/f/6/9/2/6927d190ab37c774b59b4940b06bc90b82.png "$\[\sum\limits_{k = 0}^n {\frac{1}{{k!}}} = \frac{{e\Gamma (n + 1,1)}}{{\Gamma (n + 1)}}\]$")
.
.