13. Пусть для отображений

,

отображение

тождественно. Верно ли, что

?
Попытка №2.
Ответ. Нет, не верно. Контрпример:

Здесь

,

и
![$\forall y \in \{ 4,5 \} [ (f \circ g)(y) = y ]$ $\forall y \in \{ 4,5 \} [ (f \circ g)(y) = y ]$](https://dxdy-04.korotkov.co.uk/f/7/5/4/754710eccf929c14f070a7da0ab14c9282.png)
. При этом

. Значит отображение

не является тождественным, и значит

не является обратным к

.
-- 03.04.2016, 11:24 --15. Доказать, что отображение обратимо тогда и только тогда, когда оно взаимно однозначно.
Доказательство.
Пусть есть отображение

.
Доказательство

.
По определению, взаимно однозначность

значит что

множество

состоит из одного элемента. Построим отображение

, которое каждому

ставит в соответствие этот самый единственный

из его прообраза

.
Пусть
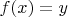
для произвольного

. Тогда

и

Таким образом, отображения

и

- тождественные, и значит отображение

является обратным к

.
Доказательство

.
По определению обратимости

существует отображение

, такое что отображения

и

- тождественные.
Пусть
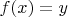
для произвольного

. Тогда

т.е.

есть построенное в первой части доказательства отображение, ставящее каждому

в соответствие единственный

из

. Тот факт что такой

единственный, следует из определения отображения. Если бы

не был единственным, отображение

не было бы определено. Таким образом,

взаимно однозначно.



