Извините, долго печатал текст, давно упустил нить дискуссии, и потому вклиниваюсь, наверное, невпопад, и может быть вообще зря

.
Насколько я смог понять первые посты топикстартера (если что не так, то прошу извинить, ведь я не "зубр", а простой ограниченный "Синус", мои мысли не взлетают высоко), поначалу ТС хотел полностью
избежав изучения спина обнаружить автоматическое появление "детерминантов Слетера" и "бозон/фермионной статистики" в задачке о 2-мерном изотропном осцилляторе. Поводом ему послужило его наблюдение, что вырожденность спектра в этой задачке позволяет строить собственный функции, обладающие чётностью или нечётностью к перестановке аргументов

Ответ был дан: без понятия
спин ни в какой задаче не появятся те настоящие бозоны/фермионы, о которых пишут учебники (причём, спин в реальной физике напрямую связан с рассмотрением вращений в
3-мерном пространстве, даже если речь идёт о частицах со спином равным нулю). Без спина можно лишь, подобно тому как дети в песочнице "пекут куличики" из песка подражая взрослым, испечь игрушечные "бозоны/фермионы" из чисто орбитальных 1-частичных волн. функций: можно
по своему произволу своими руками налагать условие определённой симметрии к перестановкам на
произвольно составленные N-кратные произведения 1-частичных в.ф. Математика не заставляет это делать, но и не запрещает так "потренироваться на кошечках", поиграть во взрослых дядей (которые делают "нечто похожее", но делают осмысленно - со спином, как это и рассказано в учебниках. Позже, может быть, приведу для ясности цитаты из книжек, поскольку ТС вроде и книжками недоволен).
А теперь вернусь к 1-частичной задачке (хотя и допускающей 2-частичную интерпретацию, но, как станет ясно, ценой потери физической содержательности преобразований симметрии в этой задаче) - к
двумерному изотропному гармоническому очциллятору из
первого поста ТС. И приведу
элементарные примеры, показывающие, из каких соображений в той или иной ситуации мы отдаём предпочтение определённому выбору полного ортонормированного набора с.ф. из бесконеного множества разных возможных выборов при вырожденном спектре.
Топикстартеру это, может, уже не нужно, если его вопросы были лишь о происхождении бозонов и фермионов, но вдруг тему посмотрит какой-нибудь начинающий студент, и, как это иногда бывает, спросит: "блин, раз из-за вырождения есть бесконечно много спсобов выбрать набор базисных функций, то чё делать-то, какой набор с.ф. лучший?"
(Часть 1. Симметрия полная, нет возмущения)
Сначала чуток подправлю гамильтониан

: формулы для энергии, приведённые ТС (и
мной), верны, если в

включён коэффициент

это соответствует выбору:



при этом декартовы координаты

мы измеряем в единицах длины

энергию

измеряем в единицах

И минус в первых слагаемых

у ТС был потерян:

Этот

инвариантен к преобразованиям координат нескольких видов (его преобразования симметрии). И поэтому мы можем выдвинуть дополнительное требование к с.ф. гамильтониана: чтобы с.ф. были собственными и для оператора того или иного преобразования симметрии (в учебниках об этом написано примерно так: "базисные функции энергетического представления выбираются как с.ф. для

и одновременно для полного набора операторов, коммутирующих с

и друг с другом").
1) Заметим для начала, что наш

инвариантен к операциям изменения направлений координатных осей на противоположные (каждой отдельно или обеих сразу):


Это можно трактовать как отражения относительно x-оси или y-оси. Собственные значения таких операторов есть

Вот и потребуем, чтобы с.ф.

обладали чётностью (либо нечётностью) к этим отражениям. Тогда годятся с.ф. вида (пишу их с нормировочным мн-лем):

поскольку полиномы Эрмита как раз имеют желаемое свойство:

Спектр энергии складывается из энергий двух 1-мерных осцилляторных степеней свободы:

уровни здесь

-кратно вырождены.
"Синус" стремится к простоте и потому вместо общих формул (и вместо полного исследования задачи) ниже рассматривает только основное состояние и 1-й возбуждённый уровень

. А так как речь пойдёт и о теории возмущений, то заранее припишем метку

этим пока ещё невозмущённым уровням:
Уровню

принадлежит с.ф.

обозначим её как

или проще:

Уровню

аналогично принадлежат две с.ф.:

и

2) Наш

инвариантен также к поворотам координатных осей в плоскости

(на произвольный угол

скажем, против часовой стрелки вокруг воображаемой третьей декартовой оси

Рассмотрим пока только такие новые оси

которые повёрнуты на

так что новые координатные переменные есть:

Ясно, что

инвариантен к отражениям относительно новых осей. Из рисунка (нарисовать его здесь я поленился)) видно, что отражение относительно оси

переставляет оси

местами. Вот пусть второй возможный наш выбор системы с.ф. и заключается в требовании определённой чётности с.ф. к перемене местами

Применительно к в.ф. основного и 1-го возбуждённого уровня находим:
Уровню

принадлежит прежняя симметричная с.ф.

Уровню

принадлежат две "детерминантно-образные" с.ф.:
симметричная

то есть

антисимметричная

т.е.

3) Инвариантность

к поворотам в плоскости

на произвольный угол

(её можно было бы использовать для разделения переменных в полярных координатах) проявляется также в коммутативности

с оператором

, совпадающим по виду с оператором проекции орбитального момента импульса


Вот третий наш способ выбора системы с.ф. пусть и заключается в построении из с.ф.

линейных комбинаций

, являющихся собственными функциями этого оператора:

Как видно из

, оператор

антисимметричен к перестановке

поэтому результат его действия на симметричную функцию заведомо будет равен нулю, т.е. симметричные функции являются для него собственными с собственным значением

Значит, с.ф. основного состояния

, инвариантная к поворотам

уже есть собственная для

с

и можно обозначить её как

Применяя явно операции взятия производных в

легко проверить (достаточно дифференцировать только предэкспоненту), что следующие две линейные комбинации из функций 1-го возбуждённого уровня тоже есть с.ф. для


принадлежит с.зн.


принадлежит с.зн.

то есть уровню

принадлежат две с.ф.:


На этом остановлюсь. Отчёт: привёл три примера конкретного выбора коэффициентов

в общей
формуле, представляющей с.ф. вырожденного уровня в виде линейных комбинаций с.ф.

с фиксированным


В примере 1) только одиночные коэффициенты отличны от нуля, они равны единице. В примере 2) для первого возбуждённого уровня не равны нулю два вещественных коэффициента в каждой из двух линейных комбинаций, а сами комбинации "детерминанто-образны". В примере 3) коэффициенты оказались комплексными. Выбор вариантов у нас определился тем, какой из симметрий гамильтониана мы отдаём предпочтение.
(Часть 2. Возмущение понижает симметрию)
"А какая же из симметрий предпочтительна?" - может теперь спросить начинающий студент. "Синус" представляет себе ответ так: в любой реальной физической задаче симметрия скорее всего не идеальная, она нарушается, например, какими-нибудь внешними полями. Поэтому разобрав учебную задачку об изотропном осцилляторе, мы не должны повесить результат на стенку в красивой рамочке и вечно им любоваться, а должны подумать: что изменится, если включить хотя бы слабенькое возмущение. "Синус" разберёт, конечно, только самые элементарные примеры возмущения, в которых результат интуитивно очевиден, а расчёт "по теории возмущений" по-детски лёгкий

.
Как и в "Части 1" выше, рассматриваем только основное состояние и первый (2-кратно вырожденный) уровень энергии, притом ограничиваемся только первым порядком малости по возмущению.
1) Пусть у реального осциллятора частота колебаний вдоль осей

оказалась не точно одинаковой. То есть, 2-мерный потенциал теперь имеет вид (при том, что масса осциллятора равна единице):

где

- малая добавка к

Раскрыв скобку и отбрасывая член второго порядка малости, получим:

С такой точностью возмущающая добавка

к исходному гамильтониану

имеет вид:

Ясно, что энергия по-прежнему даётся суммой энергий 1-мерных осцилляторов, но у них теперь чуть-чуть разные масштабы длины и разные кванты энергии, т.к. их частоты слегка разнятся. У x-осциллятора квантом энергии будет

а у y-осциллятора прежний квант энергии:

Поэтому сразу же можем записать формулу для возмущённых уровней с поправками первой степени по


Как видим, вырождение снято. Основной уровень и расщепившийся дублет 1-го возбуждённого состояния теперь таковы:



Цель дальнейшего рассказа - элементарно иллюстрировать тот факт, что "с учётом реальности" (т.е. с учётом возмущения, нарушающего высокую симметрию исходного

), нам не надо больше "руками" выбирать между равноправными базисами: возмущение само отберёт
правильные линейные комбинации волновых функций нулевого приближения.
Согласно правилам теории возмущений, первая поправка

к уровню основного состояния (невырожденному, так что мы пишем это просто для разминки) вычисляется по формуле

При вычислении таких интегралов нам достаточно будет учитывать нормированность (и, если потребуется, взаимную ортогональность) в.ф. одномерных осцилляторов, а также пользоваться формулами для матричных элементов оператора координаты, известными из задач об 1-мерном осцилляторе:


и т.п. Находим таким образом:

и в сумме с вкладом нулевого приближения

получаем верный ответ:

Согласно правилам "теории возмущений с вырождением", для 2-кратно вырожденного уровня надо вычислить 2х2-матрицу

пользуясь любым известным нам базисом нулевого приближения. Начнём с простейшего нашего базиса - с функций

(см. обозначения в нашей "Части 1"); имеем:


В этом базисе матрица

оказалась диагональной. Сл-но, данный базис уже
правильный для данного возмущения, и диагональные элементы являются искомыми поправками к вырожденному уровню:


заранее известный ответ

благополучно воспроизвёлся.
Если же начнём с "симметрично-антисимметричного" базиса

то придём к недиагональной матрице:

Однако секулярное уравнение

даёт для

прежние два корня

и

а соответствующие им правильные функции оказываются суммой и разностью функций

так что вместо "детерминантных" функций

автоматически возникают обычные

и

то есть:

- собственная ф-я для уровня


- собственная ф-я для уровня

Вот это факт и хотелось показать: в данном примере возмущением снялось вырождение и разрушились "детерминантные" функции, хотя до того они нам почему-либо могли нравиться в качестве базисных функций нулевого приближения. И понятно, отчего так вышло: как пояснено в "Части 1", "детерминантные" функции были возможны из-за того, что повёрнутые на

оси, т.е. оси

были равноценны исходным

. Возмущение

уничтожило исходную симметрию к отражению относительно

а симметрия к отражению относительно осей

сохранилась. Правильные функции, т.е.

и

автоматически обладают определённой чётностью к сохранившемуся отражению.
2) Чтобы подтвердить разумность сих нехитрых мыслей, рассмотрим другое возмущение первоначального изотропного осциллятора - пусть теперь возмущение привносит разницу в частоты колебаний вдоль повёрнутых на

осей, т.е. вдоль

(см.


Интуиция подсказывает, что теперь правильными базисными функциями должны оказаться как раз "детерминантные"
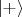
и

С учётом формул

легко вычисляем матрицу оператора возмущения

в простом базисе

и





Секулярное уравнение

снова даёт для

знакомые нам два корня:

и

Соответствующие им правильные функции

определяемые из системы уравнений


как и ожидалось, автоматически оказываются "детерминантными":

для


для

3) Ну и в завершение посмотрим, как возмущение приводит к комплексным с.ф.

из нашей "Части 1".
Вернёмся к исходному двумерному изотропному

-осциллятору, и предположим, что он имеет электрический заряд

Включим вдоль

сла-а-абенькое однородное магнитное поле

Тогда оператор обобщённого импульса

заменится оператором

Множитель

включим в

т.е. положим

и

Калибровку векторного потенциала, обеспечивающую равенство

можем выбрать так:

Тогда возмущённый гамильтониан принимает вид:


Для поиска решений в низшем порядке теории возмущений отбросим члены второго порядка малости, пропорциональные

Тогда возмущённый гамильтониан запишется как сумма прежнего невозмущённого

и возмущения

вида:

где

- тот самый оператор момента

который обсуждался в нашей "Части 1". Тут и к бабке не ходи: сразу ясно, что для диагонализации матрицы

надо правильные функции нулевого приближения выбрать в виде собственных функций

и

рассмотренные в "Части 1" (напомню: речь идёт о 2-кратно вырожденном (в отсутствие возмущения) первом возбуждённом уровне). Если начать с другого базиса, то диагонализация матрицы возмущения всё равно приведёт нас именно к ним.
В этом примере поправка первого порядка по магнитному полю

к энергии первого возбуждённого уровня имеет вид

она снимает вырождение и описывает "эффект Зеемана" - изменение энергетического спектра под действием магнитного поля. (В данном примере это пока что игрушечный эффект; ибо для реальных электронов наряду с орбитальным моментом столь же важную роль играет ещё и спиновый магнитный момент.)
Таким образом, здесь я попытался конкретно пояснить, что та или иная симметрия орбитальных волновых функций в одночастичной (хотя и неодномерной) задаче легко разрушается незамысловатым возмущением. И, в частности, уже поэтому она не может служить основой для такой фундаментальной классификации частиц как "бозоны/фермионы".
Симметрия же или антисимметрия многочастичных состояний к перестановкам полных наборов квантовых чисел 1-частичных состояний, которая рассматривается в "методе вторичного квантования" в нерелятивистской КМ и в релятивистских КТП и которая ведёт к бозе- и ферми-статистикам, основана
на тождественности частиц, устойчивой ко всяким возмущениям (о статистиках вообще должен вестись отдельный большой учебно-воспитательный разговор, а точнее - учащийся человек должен изучить
последовательно всё, написанное по данной теме в книгах, не делая для себя скоропалительных выводов лишь из отдельных фраз).
Возмущающие поля меняют вид гамильтониана и форму орбитальной части 1-частичных в.ф., но не портят тождественность частиц одинакового сорта, ответственную за возможность классификации частиц на "бозоны/фермионы" (Вот в таком смысле и говорилось выше, что вид 1-частичного гамильтониана и форма координатно-зависящей части 1-частичных в.ф. несущественны при обсуждении "бозонов/фермионов"). Симметрия либо антисимметрия
многочастичной в.ф. к перестановкам тождественных частиц, как показал разнообразнейший физический опыт, это всегда
точная симметрия.