Я так и не понял каким образом приходят к распределению Вейбулла и с какого потолка падает степенная зависимость.
Я решил посмотреть интенсивность отказов для модели
Каждое устройство изготавливается с дефектом с некоторой вероятностью

. Если устройство получилось бракованным, то вероятность выхода его из строя

, если без дефекта - то

. Эта модель даёт два первых участка кривой. Далее, начиная с некоторого момента времени

вероятность

возрастает со временем по некоторому закону
На первом участке зависимости выходят из строя все бракованные изделия и на участках нормальной эксплуатации и старения остаются только не бракованные. Вот с этих участков я и начну.
Интенсивность отказов определяется по формуле

, где

- количество вышедших из строя изделий за интервал наблюдения от

до

,

- количество исправных изделий на момент времени

. Полагая вероятность выхода из строя

, а количество изделий на момент времени

большим, скажем, что

, в знаменателе пренебрежём

, так, что

. (Предположение о том, что

несколько ограничивает наши рассуждения в период старения, когда изделий становится мало. Будем считать, что мы не рассматриваем такую ситуацию.)
В каждом конкретном жизненном цикле изделий мы можем получить не в точности график интенсивности отказов, а реализацию случайного процесса, математическим ожиданием которого и является

, то есть

Интенсивность отказов, таким образом, на этапе нормальной эксплуатации и в период старения повторяет зависимость

. Там, где вероятность выхода из строя изделия от времени не зависит, остаётся постоянной и интенсивность отказов. Там, где

возрастает в связи с износом - возрастает и интенсивность отказов.
Теперь период приработки. На этом этапе на интервале от

до

отказывают

бракованных и

небракованных изделий поэтому

. Усредняя по ансамблю жизненных циклов (рассмаривая многократные повторения жизненных циклов изделий), запишем:

Рассмотрим первое слагаемое

:
Обозначив

- количество бракованных изделий, в начальный момент времени запишем:

На следующем шаге в среднем

а вот общее количество изделий будем считать неизменным (пренебрежём количеством вышедших из строя по сравнению с общим количеством на всём периоде приработки), тогда


...
На

-м шаге

Полагая в среднем

, получим

Результирующая зависимость для кривой интенсивности отказов в дискретном времени:

Результаты моделирования при

;

;

; усреднение по 10 жизненным циклам. Сплошной красной линией показана полученная зависимость.
1.

,

- параметр,

- порог старения,

- функция Хевисайда
Вложение:
Комментарий к файлу: Интенсивность отказов 1
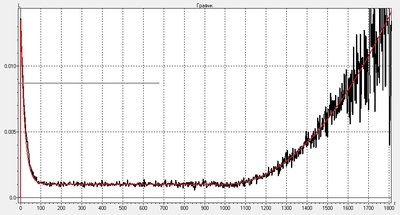 1.jpg [ 130.31 Кб | Просмотров: 0 ]
1.jpg [ 130.31 Кб | Просмотров: 0 ]
2.


- параметры
Вложение:
Комментарий к файлу: Интенсивность отказов 2
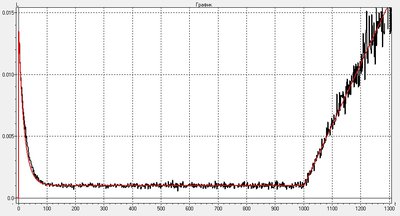 2.jpg [ 112.08 Кб | Просмотров: 0 ]
2.jpg [ 112.08 Кб | Просмотров: 0 ]
3.

при

и

при

.
Вложение:
Комментарий к файлу: Интенсивность отказов 3
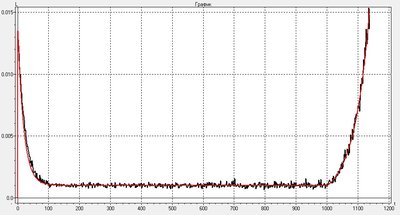 3.jpg [ 105.13 Кб | Просмотров: 0 ]
3.jpg [ 105.13 Кб | Просмотров: 0 ]



