Возвращаюсь к картинкам электрического поля с двумя проводами. Оказывается, эта учебно-воспитательная задачка встречается чуть ли не в каждом задачнике, ибо по счастливому случаю она имеет совсем элементарное решение.
Представим себе вместо проводов конечного радиуса

с расстоянием между центрами

аналогичные две параллельные
нити на каком-то расстоянии

друг от друга; ес-нно, с линейной плотностью заряда

и

Вот уж в случае нитей-то (исчезающе малого радиуса и бесконечной длины), без сомненья, можно найти электрическое поле "по суперпозиции", через простые формулы одиночных нитей. Суммарный потенциал двух нитей в точке наблюдения

есть (выписываю его без несущественной аддитивной постоянной, которую при желании можно было бы использовать для обезразмеривания аргументов логарифмов):

, где

,

.
Уравнение эквипотенциальных поверхностей (линий на плоскости

на которых

) есть

, где

- числовой параметр.
К нашему удовольствию это уравнение представляется в форме уравнения
окружности:

с радиусом

квадрат которого есть

.
При этом смещение центра окружности по оси

, т.е. величина

может быть приравнена к заданному

или

Из этих условий находим половину расстояния между нитями

при котором эквипотенциальные поверхности оказываются как раз на месте поверхностей наших исходных проводов:

.
Как видно (и такой результат понятен), расстояние

немного меньше расстояния между центрами проводов
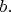
Расчёт электрического поля между проводами этим методом (т.е. как поля между нитями) показал, что при

исправленные картинки для электрического поля и вектора Пойнтинга визуально очень мало отличаются от приведённых выше картинок, поэтому я их здесь не помещаю. Помещаю только картинку эквипотенциальных контуров вокруг нитей; жирные окружности изображают положение поверхностей проводов (затем при расчете поля идеальных проводов

я внутри обоих кругов его обнуляю руками):

(И вот ещё картинки из аналогичных подсчётов (методом "изображающих нитей") при b=3a:)
Эквипотенциальные контуры нитей и положение поверхностей проводов при

:

Электрическое поле при

:

Магнитное поле при

снаружи проводов (а внутри проводов оно не изображено, как и раньше, т.к. внутри проводов оно всё равно не даёт вклада в вектор Пойнтинга):

Величина вектора Пойнтинга (плотность потока энергии) при

:




