Ну данном случае можете сами решать, как рассматривать эту ситуацию и относительно какой позиции.
ну вот я решаю нарисовать прямую не вправо-вверх как вы, а влево вниз. все же точки на окружности равноправны. получаю что вторая окружность наоборот больше
это бессмысленный рисунок, что нарисовать больше а что меньше вы выбираете совершенно волюнтаристски. потому-что то что в одной исо нарисовано как один момент, в другой исо придется рисовать как временной промежуток, а не мгновенную картинку. а вы из этого временного промежутка выбираете наугад один момент и рисуете картинку для него
При этом масштабы длины и «пространства-времени» системы K’ для каждого направления в СТО подбираются таким образом, чтобы при пересчёте в систему K они давали точно такие же численные значения, какое даёт классическое течение времени.
Но в СТО, тем не менее, такая сфера строится. Как это реализуется? А делается это так: в каждом направлении прямой, соединяющей точку O с поверхностью сферы радиуса

, с центром в точке O' в системе K' меняется масштаб длины и масштаб времени так, что

, пересчитанное в масштаб длины «неподвижной» системы K, это расстояние от точки O' до поверхности сферы, например отрезок O'E . Для сохранения условия

надо чтобы dt’ изменилась в той же пропорции. То есть

.
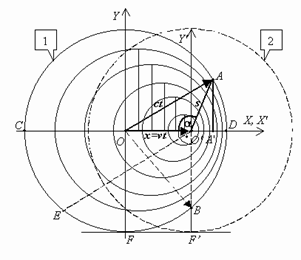
Отсюда видим, что в направлении O'E масштаб длины и «пространства-времени» в системе K' должны сократиться, в направлении OE – увеличиться, а в каждом из промежуточных направлений принять некоторое промежуточное значение.



