Вы справились с первым пунктом?
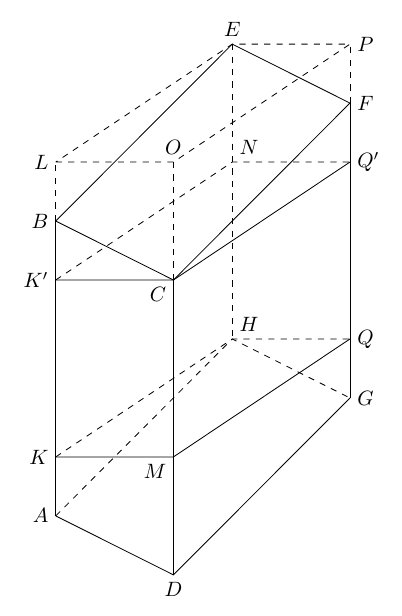

- это сечение перпендикулярное рёбрам

,

,

,

, расположенное в горизонтальной плоскости максимально "внизу" фигуры.

- то же самое сечение

, но сдвинутое максимально "вверх" до упора.

- это тот же параллелепипед о котором говорилось в начале треда, но повёрнутый чуть по-другому. Как ни поворачивай гипотетическое тело в гипотетическом пространстве - оно (тело) всегда будет сохранять прежний объём и площадь поверхности.
Упражнение: обосновать, что объём и боковая поверхность от этого не изменятся.
Поскольку

,

,

и

- рёбра параллелепипеда

, то следовательно эти рёбра параллельны друг другу и равны между собой. Обозначим через

длину одного ребра. Два перпендикулярных рёбрам сечения

и

отрезают от параллелепипеда

маленький параллелепипед

с рёбрами

,

,

и

, обозначим длину одного ребра маленького параллелепипеда как

. Отсюда длина отрезка

равна

, но, если от

отнять

мы получим следующее:

, то есть, результат равен

. Аналогично получается, что

и

. Теперь, фигуру

сдвинем параллельно "вверх" и совместим с фигурой

так, что точка

совместится с точкой

, точка

совместится с точкой

, точка

с точкой

и точка

с точкой

и получим прямую призму

(выровняли связку карандашей). Поскольку в сумме фигуры

,

и

обладают тем же объёмом, что и параллелепипед

, то получившаяся прямая призма

по объёму равна параллелепипеду

, причём

, то есть равно длине ребра параллелепипеда

. Объём прямой призмы равен произведению площади основания на высоту, то есть произведению перпендикулярного сечения параллелепипеда

на грань параллелепипеда

. Теперь что касается боковой площади. Площадь параллелограмма равна произведению основания на высоту. Площадь боковой поверхности параллелепипеда

равна

, где

- периметр сечения

. В прямой призме

боковая поверхность равна сумме площадей прямоугольников

,

,

,

, то есть

, где

- периметр сечения

, а

. Значит площадь боковой поверхности параллелепипеда

и прямой призмы

одна и та же. Принимаете доказательство?