Условие:В наклонном параллелепипеде проекция бокового ребра на плоскость основания равна

дециметров, а высота равна

дециметров. Сечение, перпендикулярное боковому ребру, есть ромб с площадью

квадратных дециметра и диагональю, равной

дециметров. Найти боковую поверхность и объём параллелепипеда.
Ответ: 
квадратных дециметров и

кубических дециметров.
Моё решение:Как я вижу фигуру:
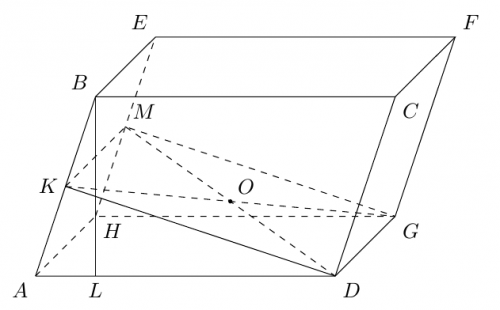
Здесь

,

,

,

,

,

,

и

- прямоугольники.

и

- параллелограммы.

- ромб, правда на моём чертеже это не очевидно. Из условия задачи

дециметров,

дециметров,

квадратных дециметра и

дециметров.

квадратных дециметра. Поскольку

, то

дециметра.

дециметров;

дециметров.

дециметров.

;

дециметра. Объём параллелепипеда выражается формулой:

, где

- объём,

- площадь основания,

- высота параллелепипеда.

.

дециметров.

кубических дециметров.

квадратных дециметров.

квадратных дециметров. Площадь боковой поверхности равна:

квадратных дециметров. Объём не сходится с ответом данным в задачнике. Пожалуйста, подскажите где я ошибся?