А вот попробуйте сделать то же самое в вырожденном случае, когда все 4 заданные точки лежат на одной окружности и посмотрите что получится.
Именно это я и попробовал. Картинки - результат малых отклонений от четырех окружностей.
Похоже, что пересечению ГМТ вне четырёхугольника

соответствует четырёхугольник с самопересечением.
Ну уж вне не исходного, а получающегося четырехугольника - точно:
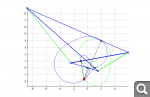
Интересно было бы сделать игрушку, в которой данные точки можно таскать мышкой и смотреть
Спасибо, интересная идея.
Вот пример вырожденного четырехугольника - правая нижняя вершина улетает в бесконечность:
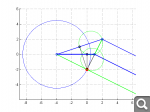
Если исходные 4 точки лежат на одной окружности, то вся эта окружность является решением системы (обе кривые ГМТ ее содержат), но при этом результирующий четырехугольник вырождается в точку на этой окружности, диаметрально противоположную точке, выбранной в качестве решения.