Конечная десятичная дробь

[m_victor]

Для каких натуральных $n$ дробь $\frac{4n+1}{n(2n-1)}$ представима в виде конечной десятичной дроби (кдд)?

Обыкновенная дробь представима в виде кдд если она имеет вид $\frac{q}{2^a\cdot5^b}$
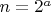
Мою дробь можно написать как $\frac{6}{2n-1}-\frac{1}{n}$. Чтобы разность была кдд, уменьшаемое и вычитаемое тоже должны быть кдд. Так как $2n-1$ нечетно, $2n-1=3$ или $2n-1=5^b\cdot3^c$, $c\in\{0,1\}$. Если $2n-1$ делится на $5$, $n$ не делится, т.е. $n=2^a$. Насколько я понимаю, задача сводится к решению уравнения $2^{a+1}-1=5^b\cdot3^c$, $c\in\{0,1\}$. Как доказать, что кроме $0, 1$ и $3$ никакие $a$ не подходят?

(Оффтоп)

Прогнал в экселе все $n<200$, подошли только $1, 2, 8$.

[iifat]

m_victor в сообщении #831392 писал(а):

Чтобы разность была кдд, уменьшаемое и вычитаемое тоже должны быть кдд

Таки $\frac23-\frac16=\frac12$

-- 01.03.2014, 02:21 --

Мне кажется, расписывать как разность бесполезно. Это только усложняет вопрос.
$\text{НОД}(n,4n+1)=1$; $\text{НОД}(2n-1,4n+1) = \text{НОД}(2n-1,3)$. Таким образом, дробь сократима на 3 либо несократима. Отсюда можно и поплясать дале.

[Cash]

Надо поподбирать модули по которым это уравнение не будет иметь решений, кроме некоторых.
Например, $2^{a+1}-1=5^b$
рассматриваем по модулю $4$.
Решение только $(0; 0)$

-- Пт фев 28, 2014 19:24:25 --

iifat в сообщении #831410 писал(а):

Таки $\frac23-\frac16=\frac12$

Если знаменатели взаимно просты, то рассуждение проходит.