Я так понял, что речь шла о том, что можно восстановить по трехмерному тензору

четырехмерный метрический

по приведенным соотношениям, нет? (индексы я взял, как у ЛЛ).
Нельзя, и вряд ли об этом шла речь. Да, если попытаться, 4 уравнений будет не хватать, тут вы совершенно правы.
Или Bulinator вообще не об этом говорил?
Думаю, не об этом. Он говорил о дальнейших расчётах в рамках трёхмерия.
-- 12.11.2013 22:27:17 --Однако же в популярных статьях прочёл, что наш мир плоский. Интересно в каком смысле это понимать?
Вот. Это совершенно другой вопрос.
Из всех способов провести в нашей 4-мерной Вселенной какое-то мысленное 3-мерие, есть один выделенный. Это способ, в котором 3-мерие будет обладать свойствами однородности и изотропности. Грубо говоря, мы отмеряем от точки Большого Взрыва "окружность", откладывая равные промежутки времени, во все пространственные точки Вселенной. Хотя это больше похоже на откладывание расстояний от вершины конуса.
И вот такое 3-мерие считается "стандартным" в космологии, и именно его подразумевают, когда говорят, что "Вселенная плоская", или "с положительной кривизной", или "с отрицательной кривизной". Хотя такое употребление слов, без уточнений "трёхмерная кривизна" или ссылок на модель Фридмана-Леметра, всё равно бывает только в популярной литературе.
Однако, как это определили?
Очень просто, и очень сложно. Просто: наблюдали в телескоп то, что видно во Вселенной, и сравнивали с расчётами для моделей "плоской", "с положительной кривизной", "с отрицательной кривизной". Но сами эти расчёты сложны.
(Вот, например, картинко)
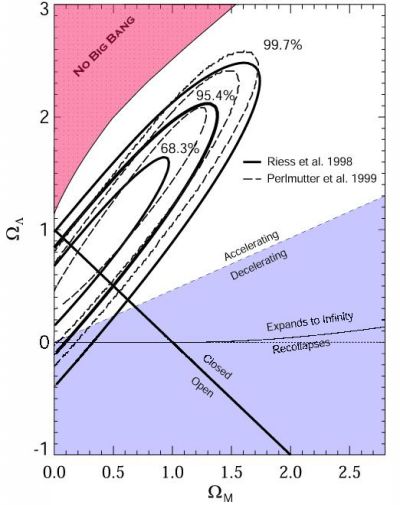
Линии по диагонали, отмеченные словами "Open" / "Closed" - это как раз разные величины трёхмерной кривизны. Сама линия между "Open" и "Closed" соответствует "Flat" - точно плоской Вселенной.
Иногда в популярных книжках описывается такая процедура. Допустим, мы живём в однородном лесу. И давайте посчитаем количество деревьев в пределах радиуса 1 км от нашего дома, в пределах радиуса 2 км, 3 км, и так далее. На равнине мы будем иметь

На холме мы будем иметь убывающую функцию

а на перевале между холмами - наоборот, возрастающую -

Здесь коэффициент

есть секториальная кривизна в той точке, где мы находимся.
И действительно, астрономы поначалу пробовали такой простой подход, со звёздами и галактиками. Но поначалу он ни к чему не приводил, а если добираться до очень больших расстояний (миллиарды световых лет), то возникает дополнительный эффект: мы видим вдалеке галактики в те времена, когда Вселенная была моложе и меньше, и галактики были ближе друг к другу. Поэтому даже в плоской Вселенной появляются поправки к формуле

Чтобы их всё-таки полноценно учесть, надо рассчитывать космологическую модель - то есть, мы возвращаемся к сложному методу.
Но если мир сегодня плоский, не факт, что это было так вчера (поскольку влияние чёрной энергии возрастает).
Факт. Эта величина - константа со временем.
Вообщем всё оказалось сложнее, чем можно понять, особо не вникая в суть дела.
"Вообщем", вникайте! Книги по космологии можно взять, например, здесь:
«Литература по астрономии: аннотированный список»(только учтите, что нужен ещё и курс молодого бойца по ОТО - это, например, здесь:
«Ищу литературу по…»).