profrotter писал(а):
Вот я опять открываю Фихтенгольца том 1 и на стр.498 нахожу формулу:

Ничего мне не мешает рассматривать эту формулу на целых числах:

и, в частности, при

и записать

, Вы решили некоторым способом примерно такую задачу (я немного обобщу её).
Функции

и

аналитичны в окрестности точки

(разлагаются в ряд Тейлора, сходящийся к соответствующей функции). Обе функции обращаются в нуль при

. Из-за этого функция

не определена в точке

, однако похоже, что доопределением

в нуле можно сделать её непрерывной. Пользуясь разложением в ряд Тейлора, найти нужное значение в нуле.
Решали Вы её примерно так.
Так как

,

, ряды Тейлора для

и

в точке

начинаются с первой степени

:

,

.
Подставим разложения в дробь и сократим на

:

Теперь числитель и знаменатель не обращаются в нуль при

(по крайней мере, в нашем случае). Мы подставляем

и находим:

.
Получается, что ряды Тейлора целиком не нужны, используются только коэффициенты при первой (в нашем случае) степени

. Для знаменателя

этот коэффициент, очевидно, равен

. А откуда он берется для числителя

, если не отвечать "из книжки"?
Ответ: коэффициент при

в ряде Тейлора функции

в точке

равен

(соответственно
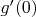
). (Производная синуса равна косинусу, а косинус в нуле равен

). Так и получается

.
Вы можете рассматривать Ваши функции на сетке, но нельзя забывать: чтобы автор Вашей книги мог записать разложение в ряд Тейлора для синуса, ему надо было определить производную, а производная -- это предел, а для вычисления предела недостаточно задать функцию на сетке. Вас не коснулись эти проблемы, потому что Вы воспользовались готовым результатом.
А вычисление отношения

, -- это в точности применение правила Лопиталя для раскрытия неопределенности вида

, то есть для нахождения предела функции

в точке, в которой

и

.
Вывод. То, что у Вас получилось -- просто классический предел функции в точке, для существования которого функция должна быть задана в окрестности

, не на сетке. Ваше дискретное рассмотрение возможно лишь на базе того, что предшественники извлекли нужную информацию (пределы, производные, ряд Тейлора) из "непрерывного" определения функции

.