Joker_vD, Вашей кашей забило важные отделы.
Sverest Давайте посмотрим на плоскость. На ней много точек, все разные. Мы хотим их все разделить на несколько классов (множест, подможеств) по определенному признаку. Например, так как

, то точка

в классе номер

(назовем его

), а так как

, то

.
Важные вопрос: сколько таких классов? Очевидно, что если взять класс

, то есть
все точки плоскости, которые удовлетворяют соотношению 
, то класс этот получится пустой. Нет таких точек на плоскости, чтобы их координаты удовлетворяли этому уравнению. Так будет для любого отрицательного числа.
Теперь, надо подумать про

. В этом классе одна лишь точка:

. Потому что если взять другую точку, то сумма квадратов будет точно больше нуля.
Классы

, где

- самые интересные. В каждом из них бесконечно много точек. Что объединяет все точки в одном классе

? то, что сумма квадратов их координат равна

. Если мы нарисуем на плоскости
все точки класса

, то нам нужно нарисовать все точки, координаты которых удовлетворяют уравнению
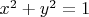
. Получится окружность радиуса

.
Отношение эквивалентности говорит, что точки эквивалентны (то есть лежат в одном классе) тогда и только тогда, когда сумма квадратов их координат одинаковая. Сумма квадратов координат - квадрат радиуса окружности, на которой лежит точка. То есть получаем:
точки эквивалентны (то есть лежат в одном классе) тогда и только тогда, когда они лежат на одной окружности. (Всюду здесь имеются ввиду окружности с центром в начале координат)