5.1. Пусть

-- группа преобразований множества

,

-- стабилизатор элемента

. Доказать, что

.
Стабилизатор элемента

включает в себя множество

(переходим в точку

, там преобразование из

точку

не меняет, а потом опять возвращаемся в

). Надо доказать, что других преобразований, кроме этих,

не включает.
Если
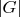
конечно, то по теореме Лагранжа

(

-- орбита

), значит

одинаково для любой точки

орбиты

, в том числе для

, т. е.

, поэтому в

не может быть других преобразований, кроме

(т. к.

).
А что делать, если

бесконечна?
-- 26 фев 2011, 20:00 --4.2. Доказать, что группа

порождается матрицами

Пусть

. Я нашёл (пальцем в небо), что

. Отсюда получаем единичную матрицу

. Сделать

не получается.
Вобщем, идея у меня такая: доказать, что

. А затем научиться из каждой матрицы из

путём умножения с одной стороны на

получить единичную. Отсюда потом получаем разложение любой матрицы из

через

, а значит, через

.