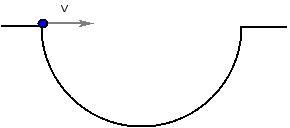
Задача, как по физике, так и по математике.
Имеется ров, каждое поперечное сечение которого -- половинка окружности радиуса

.
На одном краю находится маленький шарик с начальной горизонтальной скоростью

.
Имеется однородное поле силы тяжести с ускорением

.
Трение отсутствует, удары абсолютно упругие.
Тут несколько задач, как для детей, так и для взрослых:
а) какой должна быть величина

, чтобы время перелёта через яму было минимальным?
б) имеются ли такие значения скорости, при которых шарик не перелетит через яму?
в) как время перелёта через яму зависит от скорости

?
Решения у меня нет.
Эта задача была придумана лет пять назад в качестве иллюстрации того, чем глупая задача отличается от не глупой (длинная история, не относящаяся к делу)...
Самый лобовой способ решения -- попробовать сделать так, как с бильярдами.
То есть, можно, например, смудрить некую поверхность, по которой шарик бы двигался без изломов траектории, и сообразить, куда он попадает в результате.
Не трудно было бы выразить через скорость падения на данную точку окружности точку и скорость падения на следующую точку.
Тогда эту рекуррентную формулу можно сосчитать на компьютере численно, перебрав разные значения скорости

.
Но ведь тут есть ещё и законы физики (сумма потенциальной и кинетической энергий, например, сохраняется).
Нельзя ли их тут как-то использовать?
Есть ещё и соображения симметрии: например зависнуть-то в яме он как бы смог? -- никак?