АННОТАЦИЯ
Если в уравнении
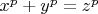
,

, переменная

- целое число, то хотя бы одно из чисел

есть иррациональное число.
Рассматривается уравнение:
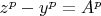
,

,
где

- целое число (простое, нечётное, чётное).
Используется разложение равенства на целочисленные множители.
В результате приходим к уравнению:
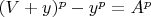
,

;
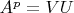
,
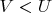
.

- целочисленные множители, на которые можно разложить целое число

при условии
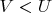
.
В полученном уравнении,

- целые числа одной чётности.
В работе показано, если переменные
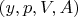
- целые числа, то данное
равенство невыполнимо для всех

.
Работа состоит из двух частей: Основная часть (77стр.) и Приложения (42стр.).
Текст работы на русском и английском языке.
Работа размещена на сайте: <fermat- theorem.net>.
Сайт находится на <google.ru>, <google.com>.
NB! Теорема доказывается в общем виде, для

.
Другими словами, все соответствующие выражения выписаны для степени

.
Если привести доказательство для

, то это будет тот же самый объём
работы. С тем различием, что все соотношения будут представлены не для
степени

, а для степени

.