Равенство

имеет место ПО ОПРЕДЕЛЕНИЮ тора. Не обсуждается.
Ради бога простите, но можно всё же высказать одно соображение. Четный тор, скажем,

, да, это сфера

c одной ручкой :

, то есть из двух 2-сфер вырезано по 2-диску (шару) и границы вырезов склеены. Нечетный же тор, скажем,

, это уже не сфера, а 3-шар

с одной ручкой - тоже шаром

, так что оба шара склеены по двум вырезанным дискам.
Поэтому, возможна и такая картина : нечетный тор

- это, согласно преемственности топологий, результат склейки двух шаров

(отрезков) по их нульмерным границам, и к сфере

может не относиться ...
-- Пн сен 27, 2010 10:02:32 --
- мерным (
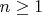
) шаром называется топологическое многообразие с краем, гомеоморфное

Скажите, а это достаточное определение для сферы

как края шара

? Если сфера односвязна?
-- Пн сен 27, 2010 10:09:19 --Край любого шара гомеоморфен сфере на единицу меньшей размерности -- это следствие ОПРЕДЕЛЕНИЙ.
Возьмем шар

. Сфера

- односвязна. Вы уверены, что край у

односвязный?
-- Пн сен 27, 2010 10:13:18 --пустое множество оттого и пусто, что в нем нет элементов:) "тем более выколотых"
Да, это ошибка, надо наверно говорить пустое множество плюс выколотая точка.
-- Пн сен 27, 2010 10:18:52 --все сферы, кроме нульмерной, односвязны... все сферы замкнуты, т.е. компактны и не имеют края
А что можно сказать про их эйлеровы характеристики? Выходит, у четных сфер двойки, а у нечётных - нули?