Применимы ли преобразования Лоренца к метрике Шварцшильда?

[manul91]

realeugene в сообщении #1666461 писал(а):

manul91 в сообщении #1666460 писал(а):

; и в сертификате о точности часов, не будет ни слова о подчинения каких-то метрик также.

Слова про точность именно это и означают.

manul91 в сообщении #1666193 писал(а):

...данной формулировки нельзя придать никакого разумного "операционального смысла", кроме как если не переопределять грубо значения слов и понятий).

Я ж знал, что в итоге все к этому придет....

[realeugene]

manul91
Если честно я так и не понял, к чему конкретно вы придрались. Каковы ваши утверждения? Что метрика не существует как объект физической теории помимо всяких часов?

[manul91]

realeugene в сообщении #1666468 писал(а):

manul91
Если честно я так и не понял, к чему конкретно вы придрались. Каковы ваши утверждения? Что метрика не существует как объект физической теории помимо всяких часов?

Запомните, дети: никакого "влияния метрики" над "хороших часов" нет!
Наоборот - все в СТО/ОТО - это о том что будут показывать как раз именно хорошие, годные часы - идущие сами по себе - без никакого над ними зловредного влияния.

P.S. Аналог: хорошая рулетка определит правильно расстояния как на плоскости так и на кривой поверхности - без никакого "влияния над ней" со стороны формы поверхности. Если поверхность влияет на рулеткой (рулетка либо сжимается, либо растягивается в зависимости где, как и на какого типа поверхности вы ее ставите) - это плохая, негодная рулетка.

[Theoristos]

epros в сообщении #1666395 писал(а):

По моим понятиям употребление слова "рассчитать" (в отличие от слова "измерить") подразумевает некую теоретическую модель. Какую теоретическую модель изменения собственного времени Вы имеете в виду, говоря о "прямом" расчёте?

Всё просто.
Вот у нас есть часы "Командирские", о 6 камнях. Со всеми шестерёнками и пружинками.
Вы их помещаете на поверхность массивного тела, и разгоняете до скорости близкой к $с$ в заданной системе отсчёта.
А теперь, исходя из знаний о шестерёнках и пружинках прямо рассчитайте скорость колебания балансира часов в таких вот условиях.

Или рассчитать равновесную длину СТО-шной линейки как набора x*y*z атомов по каждой оси, исходя из знаний законов взаимодействия атомов и транслируя их в быстро движущуюся СО.

[realeugene]

Theoristos в сообщении #1666478 писал(а):

Вот у нас есть часы "Командирские", о 6 камнях. Со всеми шестерёнками и пружинками.
Вы их помещаете на поверхность массивного тела, и разгоняете до скорости близкой к $с$ в заданной системе отсчёта.
А теперь, исходя из знаний о шестерёнках и пружинках прямо рассчитайте скорость колебания балансира часов в таких вот условиях.

Если вы их понимаете - может быть расскажете, как они будут "прямо рассчитывать скорость колебания балансира часов" без применения уравнений Эйнштейна для метрики?

-- 21.12.2024, 22:06 --

manul91 в сообщении #1666472 писал(а):

Наоборот - все в СТО/ОТО - это о том что будут показывать как раз именно хорошие, годные часы - идущие сами по себе - без никакого над ними зловредного влияния.

Нет, уравнения Эйнштейна не про часы.

-- 21.12.2024, 22:13 --

manul91 в сообщении #1666472 писал(а):

Аналог: хорошая рулетка определит правильно расстояния как на плоскости так и на кривой поверхности - без никакого "влияния над ней" со стороны формы поверхности.

Трёхмерная рулетка измерит расстояние вдоль двумерной поверхности, вложенной в трёхмерное евклидово пространство, для измерения длин в котором вдоль кривых линий и была сконструирована эта трёхмерная рулетка?

[manul91]

realeugene в сообщении #1666485 писал(а):

Нет, уравнения Эйнштейна не про часы.

Да, не все : ) Скажем так, "все в СТО/ОТО что касается показаний часов" - что и обсуждалось в нашем разговоре.

[realeugene]

manul91 в сообщении #1666486 писал(а):

Да, не все : ) Скажем так, "все в СТО/ОТО что касается показаний часов" - что и обсуждалось в нашем разговоре.

Вы не сможете рассчитать ход часов в гравитационном поле не решив уравнения Эйнштейна для метрики.

-- 21.12.2024, 22:19 --

manul91 в сообщении #1666486 писал(а):

Да, не все

И, это... А как вы собрались из них выделять часть "про часы"?

[manul91]

realeugene в сообщении #1666485 писал(а):

Трёхмерная рулетка измерит расстояние вдоль двумерной поверхности, вложенной в трёхмерное евклидово пространство, для измерения длин в котором вдоль кривых линий и была сконструирована эта трёхмерная рулетка?

realeugene в сообщении #1666487 писал(а):

Вы не сможете рассчитать ход часов в гравитационном поле не решив уравнения Эйнштейна для метрики.

realeugene в сообщении #1666487 писал(а):

И, это... А как вы собрались из них выделять часть "про часы"?

realeugene
Не буду поддерживать дальше попытки забалтывания обсуждения; смысл моих слов кристально ясен.

[realeugene]

manul91 в сообщении #1666488 писал(а):

Не буду поддерживать дальше забалтывание обсуждения; смысл моих слов кристально ясен.

Ага. Ясно, что философская фигня про "реальные часы и линейки", вместо того, чтобы использовать объекты модели ОТО непосредственно.

[manul91]

realeugene в сообщении #1666489 писал(а):

Ага. Ясно, что философская фигня про "реальные часы и линейки", вместо того, чтобы использовать объекты модели ОТО непосредственно.

Фигня не фигня, а вот после долгого ожидания оказалось что эксперт высокого класса как вы в области "оценки влияния формы метрики на точности часов" - на самом деле подрабатывает комисионами, пересылая заказы к обычных метрологов :)

[realeugene]

manul91 в сообщении #1666491 писал(а):

Фигня не фигня, а вот оказалось что эксперт высокого класса как вы в области "оценки влияния формы метрики на точности часов" - на самом деле подрабатывает на комисионы у обычных метрологов :)

Ну и опять фигню несёте.

[piksel]

piksel в сообщении #1664733 писал(а):

Этот результат может объяснить годовые изменения в дополнительном ускорении Пионера 10, см.
https://arxiv.org/pdf/gr-qc/9903024 [1],
https://arxiv.org/pdf/gr-qc/0104064.



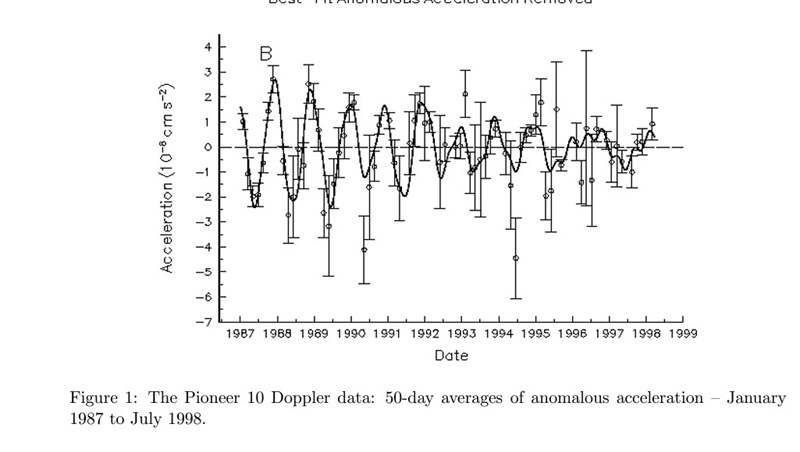
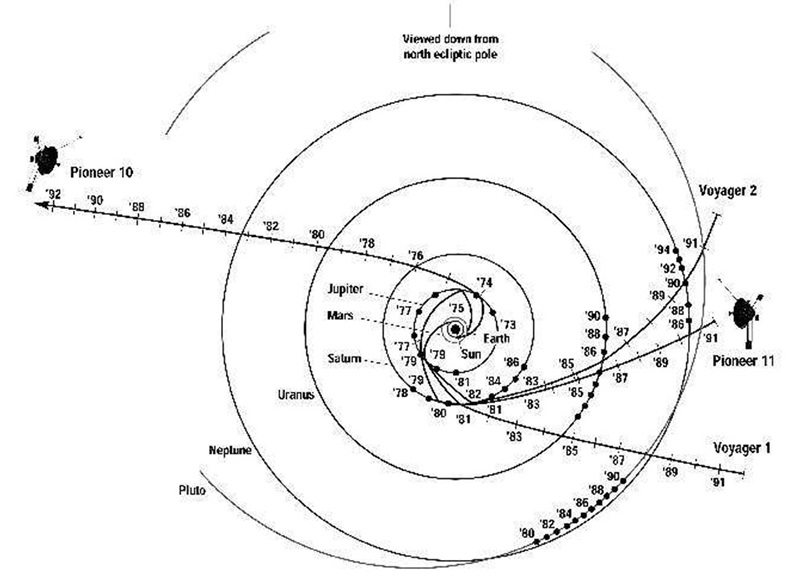
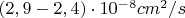
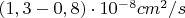
Рассмотрим ожидаемое дополнительное ускорение Pioneer 10, определенное с помощью эффекта Доплера. Оно имеет периодическую составляющую с амплитудой $ (2,9-2,4)\cdot 10^{-8} cm^2/s $ на расстоянии 40 а.е. и $ (1,3-0,8 )\cdot 10^{-8} cm^2/s $ для 60 а.е. Ускорения и расстояния определяются приблизительно по графику и схеме полета.

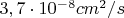
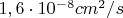
Расчеты с использованием формулы для $\frac{d^2t^\prime}{ds^{2}}$ при преобразовании в ускорение для периодической составляющей дают $ 3,7\cdot 10^{-8} cm^2/s$ на расстоянии 40 АЕ и $1,6\cdot 10^{-8} cm^2/s$ для 60 АЕ. Эти значения близки к наблюдаемым.

Пересчитал значения амплитуд колебаний сигнала в годичном ускорении с использованием данных из графика, получилось
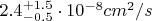
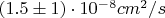
$ 2.4^{+1.5}_{-0.5}\cdot 10^{-8} cm^2/s$ на расстоянии 40 AU (1987) и $ (1.5\pm 1)\cdot 10^{-8} cm^2/s$ for 53 AU (1992).
Вторая точка взята более близко к Земле, чем в первом расчете, чтобы уменьшить вклад зашумления сигнала. Результат в пределах погрешности соответствует замедлению времени на аппарате, определяемому величиной $\frac{d^2t^\prime}{ds^{2}}$ в рассматриваемом пространстве-времени.

realeugene в сообщении #1664888 писал(а):

piksel в сообщении #1664844 писал(а):

В данном случае рассматривается не постоянная составляющая ускорения, которая была связана с тепловым излучением, а его годичные колебания.

Он же наверное постоянно направлен антенной на Землю, и качается относительно Солнца с годовым земным циклом? Из-за этого тепловое излучение тоже должно иметь годовой (земной) цикл?

На расстоянии 40-60 АЕ, поворот антенны составит 3-4 градуса от радиальной оси. Хотя антенна симметрична, но после в поворотов влево и вправо изменение частоты сигнала противоположно по знаку. В публикуемых отчетах написано, что вклад солнечного излучения учитывался.

-- Вт фев 10, 2026 16:25:55 --

Утундрий в сообщении #1665024 писал(а):

Эффект "Пионера"

Цитата:

Мы исследовали возможность аномального ускорения аппаратов «Пионер-10» и «Пионер-11» из-за силы отдачи, связанной с анизотропным испусканием теплового излучения аппаратами. Для этого, опираясь на проектную документацию, мы построили исчерпывающую теплофизическую модель конечных элементов обоих аппаратов. Потом мы численно решили уравнения теплопередачи и излучения, используя данные реальной телеметрии в качестве граничных условий. Мы использовали результаты этой модели для расчёта эффекта силы тепловой отдачи «Пионера-10» на различных гелиоцентрических дистанциях. Мы нашли, что величина, временно́е поведение и направление результирующего теплового ускорения подобны свойствам наблюдаемой аномалии. Новизна нашего исследования в том, что мы разработали параметризованную модель силы тепловой отдачи и оценили коэффициенты этой модели независимо [от теплофизической модели], по навигационным данным доплеровского слежения. Мы не нашли статистически значимой разницы между двумя оценками и считаем, что когда сила тепловой отдачи учтена точно, аномального ускорения не остаётся.

В цитируемой статье о периодической составляющей дополнительного ускорения ничего не говорится. Действительно, сложно объяснить тепловым излучением аппаратов его годичные колебания.

manul91 в сообщении #1665503 писал(а):

realeugene в сообщении #1665477 писал(а):

Нет никакой "метрики ИСО".

Пусть стандартные часы $Q$ несломаны, т.е. они работают нормально в плоском пространстве-времени - измеряют длину интервала на своей мировой линии (как бы они не двигались, в частности пусть когда двигаются с некоем собственном ускорении $a$ - оно тоже от координат/СО не зависит). Скалярная кривизна - координатный инвариант - она не зависит от выбора каких-либо координат или СО - и в плоском пространстве-времени, она равна нулю.

Потом, пусть тех же самых часов $Q$ помещают в искривленном пространстве-времени - в котором скалярная кривизна - не ноль - и они двигаются там как-то (в частности, их собственное ускорение например равно той же самой $a$ - что координатный инвариант).
Там они, точно так же измеряют длину интервала на своей мировой линии - (так как по техпаспорту производителя, в связи с устройства/испытаний этих часов, собственное ускорение $a$ вполне входит в допустимых условий использования часов в которых они помещаются в заявленную точность).

По-вашему, во втором случае, тех же самых часов $Q$ - нужно считать априори сломанными/нестандартными, или нет?
Они "последовали предписания форму метрики" в которой они были помещены (на этот раз с ненулевой скалярной кривизной), или "не последовали"?

Специально обращаю вам внимание на то, что в приведенных двух случаев области четырехмерия объективно отличаются - и это отличие совершенно не зависит от субъективного выбора каких-либо координат и/или СО.
Т.е. "вид метрики" первого многообразия в окрестности движения часов, никаким преобразованием координат/выборам СО не перевести к "вида метрики" второго многообразия в области движения часов; они объективно отличаются.
При этом вопросы к вам насчет "сломанности часов", как "форма метрики должна предписывать показания стандартных часов", в каком смысле "часам нельзя существовать независимо от метрики п-в" - остаются прежними.

Часы в системе отсчета, инерциальной, привязаны к некоторой точке, движущейся инерциально в плоском пространстве-времени, или по геодезической в искривленном п.-в. Если часы удалят из этой точки в плоском п.-в., используя ускорение, то их движение не будет инерциальным, и если их потом вернут обратно, то они будут отставать.

[Alex-Yu]

Ох, Господи... Как достали эти и подобные глупости... Запомните: в ОТО значения координат (и временной и пространственных) в общем случае не имеют вообще НИКАКОГО физического смысла. Имеет физический смысл только интервал. А он инвариантен относительно ЛЮБЫХ преобразований координат. Нет, конечно, можно выдумать некую специальную систему координат, в которой координаты будут обладать неким физическим смыслом. Но то, что в других координатах что-то там (что угодно) в координатах поменяется, вовсе не означает какого-либо физического эффекта. Потому что это уже другая система координат, в которой прежнего смысла координат уже нет.

Вообще геометрия ОТО это хроногеометрия: ВСЕ геометрические измерения делаются часами и только часами (пространственные измерения тоже делаются часами, используя абсолютный характер скорости света). Ну, можно еще углы мерить (исключительно локально!). Вот только так и никак иначе в основе своей! А интервал (вдоль мировой линии неких часов) это и есть собственное время (которое эти часы и показывают). Интервал инвариантен, значит и показания часов инвариантны. А следовательно и любые геометрические измерения тоже инвариантны, не меняются при ЛЮБОЙ замене координат. Если, конечно, не делать глупых ошибок :)

И да, еще. Эта вся ветка совершенно не в том разделе. НИЧЕГО дискуссионного тут нет. Это все чисто учебные вопросы, уместные только в разделе ПРР.

[piksel]

Alex-Yu в сообщении #1718004 писал(а):

Ох, Господи... Как достали эти и подобные глупости... Запомните: в ОТО значения координат (и временной и пространственных) в общем случае не имеют вообще НИКАКОГО физического смысла. Имеет физический смысл только интервал. А он инвариантен относительно ЛЮБЫХ преобразований координат. Нет, конечно, можно выдумать некую специальную систему координат, в которой координаты будут обладать неким физическим смыслом. Но то, что в других координатах что-то там (что угодно) в координатах поменяется, вовсе не означает какого-либо физического эффекта. Потому что это уже другая система координат, в которой прежнего смысла координат уже нет.

Вообще геометрия ОТО это хроногеометрия: ВСЕ геометрические измерения делаются часами и только часами (пространственные измерения тоже делаются часами, используя абсолютный характер скорости света). Ну, можно еще углы мерить (исключительно локально!). Вот только так и никак иначе в основе своей! А интервал (вдоль мировой линии неких часов) это и есть собственное время (которое эти часы и показывают). Интервал инвариантен, значит и показания часов инвариантны. А следовательно и любые геометрические измерения тоже инвариантны, не меняются при ЛЮБОЙ замене координат.

Это радикально, но несколько упрощенно. Действительно, интервал инвариантен, но, во-первых, задача состоит в его правильном выборе, во-вторых, все-таки, для расстояний используются единицы измерения длины, хотя мы можем пересчитать их на время, например, идти 15 минут в таком-то направлении быстрым шагом или свет долетает туда за такое-то время. Кроме того, есть и пространственно-подобные интервалы, которые не могут быть измерены передвижением вдоль них неких часов, если это не тахионные часы.

В рассматриваемом случае с помощью часов измерялась частота принимаемого сигнала от аппарата, и, соответственно, использовалась метрика, задающая интервал его движения. Безусловно, показания часов на аппарате не поменяются при выборе той или иной метрики и ее преобразовании с помощью преобразования координат.
При этом, изменение течения времени в пространстве-времени, описываемом изотропной метрикой Шварцшильда и метрикой

piksel в сообщении #1664733 писал(а):

$$ds^2=c^2\left(1-\frac{1+{{\beta}}^2}{1-{{\beta}}^2}\frac{\alpha}{r^\prime}\right)d{t^\prime}^2-\frac{4{v}}{1-{{\beta}}^2}\frac{\alpha}{r^\prime}dt^\prime dx^\prime-\left(1+\frac{1+{{\beta}}^2}{1-{{\beta}}^2}\frac{\alpha}{r^\prime}\right)d{x^\prime}^2-\left(1+\frac{\alpha}{r^\prime}\right)(d{y^\prime}^2+ d{z^\prime}^2)$$

при $\beta =v/c$ и $r' = \sqrt {{{\left( {\frac{{x' +vt'}}{{\sqrt {1 - {{\tilde \beta }^2}} }}} \right)}^2} + {{y'}^2} + {{z'}^2}}$

при малых $\beta $ и $\frac{\alpha}{r^\prime}$ без величин большего порядка малости по сравнению с $\frac{\alpha}{r^\prime ^2}$ будет описываться одной и той же формулой при замене для первой метрики $t^\prime$ на $t$

piksel в сообщении #1664733 писал(а):

$$ \frac{d^2t^\prime}{ds^{2}}=-\frac{\alpha x}{{r^\prime}^3}\frac{d(ct^\prime)}{ds}\frac{dx^\prime}{ds}-\frac{\alpha y}{{r^\prime}^3}\frac{d(ct^\prime)}{ds}\frac{dy^\prime}{ds}-\frac{\alpha z}{{r^\prime}^3}\frac{d(ct^\prime)}{ds}\frac{dz^\prime}{ds}.$$

Отмечу, что для $\beta $, приближающихся к 1 это выполняться не будет.
Однако в пространстве, описываемом изотропной метрикой, периодического изменения течения времени не будет, так как ее система отсчета привязана к центру Солнца и годичные колебания скорости аппарата в ней отсутствуют. Система отсчета второй метрики неподвижна относительно Земли и в ней аппарат имеет годичные колебания радиальной скорости, которые согласно уравнениям геодезической дают замедление времени, которое влияет на частоту испускаемого синала. Эти колебания частоты, принимаемые антенной на Земле, фиксируются расположенными на ней часами.

[Alex-Yu]

piksel в сообщении #1718015 писал(а):

но, во-первых, задача состоит в его правильном выборе, во-вторых, все-таки, для расстояний используются единицы измерения длины, хотя мы можем пересчитать их на время, например, идти 15 минут в таком-то направлении быстрым шагом или свет долетает туда за такое-то время. Кроме того, есть и пространственно-подобные интервалы, которые не могут быть измерены передвижением вдоль них неких часов, если это не тахионные часы.

Пустопорожняя болтовня, глупости. Впрочем, не Вы первый и не Вы последний. Вон Логунов целый академик был, а нес очень похожую безграмотную пургу. Так что, как говорится, флаг Вам в руки, продолжайте дальше. Но без меня.