Ну вот, и peregoudov сподобился. А я уж думал он нас совсем покинул.
Спасибо, peregoudov !
Разберём его реферат подробно.
Ну вот, а теперь о том, на что это все похоже.
А похоже это все на разводилово.
Я понимаю, что подобные тексты часто провоцируют ответ в том же стиле, чтобы свести обсуждение к скандалу — как это уже происходило и на форуме ФИАН при обсуждении подобной темы.
Я этого делать не собираюсь.
Если есть научные возражения — давайте обсуждать формулы.
Если аргументы сводятся к эпитетам — это не научная дискуссия.
Пока вместо этого я вижу эмоциональные оценки и обсуждение мотивов. Это не научная аргументация, а попытка перехода на личности.
Неудачная попытка. Цитата:
Автор начинает с правильной формулы, что мощность электростанции --- это разность потоков энергии выше и ниже по течению. И дальше начинает выдумывать в этой формуле "экстремумы", абсолютно не заботясь, чтобы они имели хоть какой-нибудь физический смысл. Выдумав такой "экстремум", автор начинает всячески раздувать "значимость" сделанного "открытия". Видимо, в надежде подороже продать.
Экстремум не «выдумывается», а получается из условия
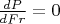
Если в выводе есть ошибка — укажите её.
Цитата:
Что косвенно подтверждается отсутствием каких бы то ни было практических применений или хотя бы наглядных демонстраций --- вот уже 20+ лет.
Практические и экспериментальные подтверждения этого предела существуют не просто 20 лет, и даже не 200.
А с тех пор как образовались реки на планете.
Все равнинные реки мира естественным образом стремятся к числам Фруда порядка 0.2–0.4, что известно из эмпирической гидравлики. Однако удовлетворительного теоретического объяснения этого факта в рамках чистого энергетического анализа до сих пор не было.
Моя работа как раз и показывает, что значение около 0.3 возникает как энергетический экстремум идеального потока.
Кроме того, фундаментальные пределы не обязаны немедленно становиться коммерческими устройствами. Предел, сформулированный Albert Betz, появился задолго до массовой ветроэнергетики. Это не аргумент против корректности вывода.
Цитата:
Видимо, первый "экстремум", F=1 в нижнем течении, стал совсем уже плохо продаваться, поэтому понадобилось выдумывать новый. Теперь это число нетривиальное --- аж целый корень уравнения третьей степени! Теперь продажи подскочат на 70%!
Это число не вводится произвольно.
Оно возникает как корень кубического уравнения, полученного из энергетического функционала.
Кстати, уточните, пожалуйста, про какие
«продажи» идёт речь ?
Цитата:
Зачем автор явился сюда --- тоже понятно и стандартно: чтобы потом всюду врать "в МГУ ничего не смогли возразить" или даже "получила апробацию в МГУ и восторженные отзывы". Ну, вот как он сейчас с других мест сюда комментарии таскает.
Я не вижу здесь специалистов МГУ.
Вижу пока лишь обезличенные ники, боящиеся показать свои фамилии.
Ничего плохого в этом нет - мало ли кому и зачем нужно скрываться под маской.
Но ассоциировать эти ники со специалистами МГУ или любыми другими специалистами нет оснований.
Поэтому и ссылаться на "мнение МГУ" нет причин.
Тем более, что и мнений то адекватных пока нет (об этом см. последнюю фразу).
Если у "специалистов МГУ" "научные" аргументы именно такие, как вы привели, то станет понятно почему эти слова взяты в кавычки

И вишенка на торте !
Цитата:
P. S. С Соколовым знаком лично. Только вот его текст на researchgate --- не про то, как все хорошо у автора. А про то, как все плохо у одного из критиков, некого Зотьева. Про сами "леневские турбины" он там отзывается весьма критически, по-русски говоря, враньем и фальсификацией экспериментальных данных называет.
Во первых, статья ИС, о которой вы говорите, размещена не на
researchgate, а на
arXiv Во вторых, я знаком с проф. ИС, вероятно, значительно лучше, чем вы. Это свидетельствует о том, что в свой препринт на arXive он положил и мою статью. Прочтите внимательно.
В третьих, - не я эту статью сюда притащил, а
вы (!).

Вероятно рассчитывая на какую то реакцию ?
Однако реакция оказалась совсем не такой, которую вы ожидали

Теперь вы вдруг заявили, что эта статья ИС совсем не про мою идею, а про критику моих оппонентов.
Так вы для этого её сюда притащили ? Чтобы моих оппонентов покритиковать ?
Вы правильно сделали – молодец ! Просто умница ! 
В четвёртых, экспериментальные данные некоей турбины (к которой я отношения не имею), о которых вы говорите, я фальсификаций назвал сразу, как только увидел. Задолго до ИС.
Но это никак не влияет на теоретические результаты и формулы, которые получены и мной, и ИС, и много кем ещё, включая даже небезызвестного вам Морозова В.Б.
В пятых, статья ИС в arXiv не только
о том, как плохо все у моих оппонентов (включая некоего Зотьева, профессора ДГТУ и пр.),
а именно и о том, что у автора все хорошо, поэтому он и положил в этот же препринт и мою статью.
Вы бы хоть прочесть то удосужились бы хотя бы,
что там написано. Хотя бы для того, чтобы в следующий раз не плюхнуться мордой в лужу.
Во время обсуждения этой темы проф. ИС высказал как-то крылатую фразу (дословно не помню, но что-то вроде этого) -
"нет лучшей поддержки теории, чем необоснованная и некомпетентная критика". Вы сейчас делаете именно это !
Умница ! 