Уважаемый
amon, ну вот, продолжу ответ на ваш комментарий.
Ваша работа базируется на бурно обсуждаемой формуле (1). ...
Откуда она взялась Вы здесь рассказать не хотите, а рыскать по старым статьям у меня, простите, времени нет. Простые проверки она выдерживает и, судя по всему, получена для невязкой жидкости (нет в ней вязкости).
Совершенно верно, вязкость в этой формуле не учтена, равно, как она не учтена в классическом Бернулли и неразрывности, а именно эти уравнения и являются базисом.
Также в этой формуле не учтены и потери.
В общем, полная аналогия с Бетцом, за исключением, что у меня присутствует гравитация и она является доминирующим вкладом в поток энергии.
Цитата:
Ваши манипуляции с приведением этой формулы к "безразмерной энергии" (на самом деле - мощности) эквивалентны следующим простым размерным оценкам..... На мой взгляд, толку от таких манипуляций немного, но могу и ошибаться.
Теперь к формулам. Коль уж к пресловутой формуле (1) ни у кого претензий нет, и нет претензий по её метаморфозам, то давайте теперь другой формулой оперировать.
Вот этой.
![$
\[
E = \rho \, L \, g^{3/2} \, H_1^{5/2} \, \Phi\!\left( Fr_1 \right)
\]$ $
\[
E = \rho \, L \, g^{3/2} \, H_1^{5/2} \, \Phi\!\left( Fr_1 \right)
\]$](https://dxdy-01.korotkov.co.uk/f/8/8/a/88a9f4aec60a4757e4900b15df29aaa382.png)

![$
\[
\Phi\!\left( Fr_1 \right)
= Fr_1 + \frac{1}{2} Fr_1^{3}
- \frac{3}{2} Fr_1^{5/3}
\]$ $
\[
\Phi\!\left( Fr_1 \right)
= Fr_1 + \frac{1}{2} Fr_1^{3}
- \frac{3}{2} Fr_1^{5/3}
\]$](https://dxdy-02.korotkov.co.uk/f/1/2/3/1239810658711a178a116e241cac790982.png)

Итак, смысл всей этой работы заключался в следующем.
Как вы верно заметили, производить метаморфозы таким образом с этими формулами можно до бесконечности и они будут принимать экзотические формы и даже с первого взгляда, возможно непохожие друг на друга по виду.
Однако единственное что от этого не изменится это форма графика который будет по ней построен.
И вот она то и вызывает наибольшее интерес.
Вот 3D диаграмма, построенная по формуле (1)
На ней видна линия экстремума.
А вот численные значения нескольких выборок
На графике видно, что функция имеет хитрую форму с двумя экстремумами.
Один из них тривиален - это
Fr=1.
А вот второй представляет наибольший интерес.
Видно, что активная глубина потока
H только масштабирует этот график по вертикали, причём:
а) масштаб меняется в степени
5/2б) точка экcтремума смещается в сторону увеличения скорости, причём тоже нелинейно, следуя некоему тренду.
И вот целью этих метаморфоз с формулами и было - выделить безразмерную функцию, которая и задаёт форму этой кривой.
Таким образом и появилась эта формула
![$
\[
\Phi\!\left( Fr_1 \right)
= Fr_1 + \frac{1}{2} Fr_1^{3}
- \frac{3}{2} Fr_1^{5/3}
\]$ $
\[
\Phi\!\left( Fr_1 \right)
= Fr_1 + \frac{1}{2} Fr_1^{3}
- \frac{3}{2} Fr_1^{5/3}
\]$](https://dxdy-02.korotkov.co.uk/f/1/2/3/1239810658711a178a116e241cac790982.png)

И экcтремум этой функции как раз и находится в точке
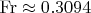
Никто до меня эту точку не находил и не видел.