Ну, нормально, чо. У вас есть главные переменные, а есть свободные, через которые главные выражаются. Так же есть условие совместности системы, при выполнение которого решение существует.
Вон, возьмите хотя бы СЛАУ из линейной алгебры:

Чтобы решение системы существовало ранг матрицы
A (не обязательно квадратной) должен совпадать с рангом расширенной (требование на "параметры" задачи):
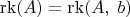
Если это выполняется, то решение существует и выражается как
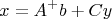
где плюсик в степени
A означает псевдообращение Мура-Пенроуза, а столбцы матрицы
C являются базисом подпространства ядра матрицы
A. Столбец
y — произвольный.
В случае нелинейных систем, всё то же самое, только больше и сложнее. Ну, в вашем случае всё разрешилось.