Равенство корней двух многочленов

[B@R5uk]

Пока из праздного любопытства (но потенциально имеющий возможность потребоваться на практике) возник следующий вопрос. Имеется два многочлена вообще говоря различной (большой) степени с рациональными (или, что почти то же самое, целочисленными) коэффициентами:

$$f\bigl(x\bigr)=\sum\limits_{k=0}^{M}a_kx^k,\qquad g\bigl(x\bigr)=\sum\limits_{k=0}^{N}b_kx^k,\qquad a_k,\;b_k\in\mathbb{Q}\;\bigl(\mathbb{Z}\bigr)$$

Определяются множества корней этих многочленов

$$S_f=\bigl\{x\in\mathbb{C}\;|\;f\bigl(x\bigr)=0\bigr\},\qquad S_g=\bigl\{x\in\mathbb{C}\;|\;g\bigl(x\bigr)=0\bigr\}$$

Существует ли метод показать, что эти два множества имеют общие элементы? Другими словами, можно ли показать, что два различных многочлена имеют одно и то же число в качестве корня? Проблема ведь в том, что явно выписать эти корни через радикалы от рациональных чисел нельзя (кроме редких случаев).

[mihaild]

Разложите оба многочлена на произведение линейных (мысленно) и посчитайте их НОД (мысленно и реально).

[ex-math]

Наверно можно поискать НОД этих многочленов с помощью алгоритма Евклида

[B@R5uk]

О! Точно. Спасибо за подсказку.

Тогда получается, если два разных многочлена с рациональными коэффициентами имеют общий корень, который не лежит в множестве рациональных чисел, то они так же имеют один или более других общих корней. Типа как наличие корня $x=\sqrt{3}$ сразу ведёт к наличию $x=-\sqrt{3}$, верно? Или могут быть разные возможности?

[dgwuqtj]

Да, если есть корень в виде иррационального числа $\alpha$, то есть и все сопряжённые с ним.

[Null]

Результант же.

[B@R5uk]

Походу, советом выше (про алгоритм Евклида) мне придётся воспользоваться раньше, чем планировалось. Проблема в том, что у меня самих полиномов ещё нет, а есть две системы из кучи квадратных уравнений на пачку неизвестных. Я их решаю численно и получаю, что одна из неизвестных в обеих системах совпадает с точностью до машинной погрешности, хотя это разные системы. Вот меня мучает вопрос: они действительно совпадают с математической точностью или же они всё-таки разные?

Есть ли какие-нибудь регулярные методы перевести систему квадратных уравнений в один полином? Или может быть есть какой-нибудь другой подход к этой проблеме?

[dgwuqtj]

Тут уже скорее нужны базисы Грёбнера.

[B@R5uk]

dgwuqtj, я когда-то про них немного читал (или пытался по крайней мере), но особо ничего не помню. Что с этими базисами применительно к моей задаче нужно делать? Может есть какая-нибудь система компьютерной алгебры, в которую можно засунуть эти две задачи и она выдаст ответ? Сомнительно, конечно, задача очень специфическая.

[venco]

B@R5uk в сообщении #1716661 писал(а):

Есть ли какие-нибудь регулярные методы перевести систему квадратных уравнений в один полином?

Сумма квадратов должна равнятся нулю, нет?
Правда, я не уверен, что алгоритм Евклида поможет, если переменных несколько.

[B@R5uk]

venco в сообщении #1716665 писал(а):

Сумма квадратов должна равнятся нулю, нет?

Не, там всё хуже и страшнее. Пачка сумм квадратов (по 3 слагаемых), действительно равняется красивому числу — единице. Другая пачка сумм квадратов разностей (ыыыыы! тоже по 3 штуки в сумме) все равняются между собой и равны квадрату особой неизвестной, которая и совпадает в двух системах. Забавно, что все константы — это только 1 и 2 (ну и 0, если пропущенные мономы учитывать или если их все налево перенести и смотреть на правую часть).

Единственный плюс системы: все мономы одинаковой степени (слева от равенства). Этот плюс быстро потеряется если пытаться исключением переменных искать полином.

[dgwuqtj]

Это задача об исключении переменных из системы полиномиальных уравнений. Вам же нужно найти, какие значения принимает одна конкретная переменная в каждой системе. В системах компьютерной алгебры имеется, но надо немножко прочитать про примеры или теорию (порядки на одночленах и как использовать базисы Грёбнера для исключения). Вместо базисов Грёбнера в принципе можно использовать результанты, но у них есть некие ограничения.

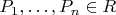
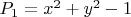
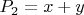
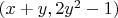
Если взять кольцо $R = \mathbb Q[x, y, z, \ldots, t]$ с лексикографическим порядком lex на одночленах, а потом посчитать базис Грёбнера набора многочленов $P_1, \ldots, P_n \in R$, то многочлены из этого базиса, зависящие только от последней переменной $t$, — это как раз результат исключения остальных переменных. Скажем, для $P_1 = x^2 + y^2 - 1$ и $P_2 = x + y$ будет базис $(x + y, 2 y^2 - 1)$, и точки пересечения прямой с окружностью как раз имеют ординаты $\pm \frac {\sqrt 2} 2$.

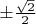
Правда, всё это работает над комплексными числами. Если надо убрать невещественные решения, то речь уже про исключение кванторов над полем вещественных чисел, там куча своих методов.

[mihaild]

venco в сообщении #1716665 писал(а):

Сумма квадратов должна равнятся нулю, нет?

Это над $\mathbb R$, а разговор, насколько я понимаю, про $\mathbb C$.

[B@R5uk]

mihaild, не, корень, который меня интересует, а так же значения остальных переменных для этого корня — всё действительные числа. Первый вопрос был для общности, я не планировал прям так сразу приступить к его практическому применению.

[B@R5uk]

dgwuqtj в сообщении #1716667 писал(а):

...то многочлены из этого базиса, зависящие только от последней переменной $t$, — это как раз результат исключения остальных переменных.

Перечитал тут по-быстрому книжку Аржанцев И.В. - Базисы Грёбнера и системы алгебраических уравнений (2003). Там нигде не заострён вопрос исключения переменных, больше упор на теорию и поясняющие задачи. Я правильно понимаю, что многочленом от одной переменной будет один из элементов базиса Грёбнера, который соответствует самой "слабой" переменной? То есть той переменной, степень которой при сравнении мономов двух многочленов (при их упорядочивании) проверяется в последнюю очередь. Просто мне надо многочлен от вполне конкретной переменной получить.