Задача про полоски с дырками

[waxtep]

Кстати, об оптимальной стратегии. Нас, кажется, явно автор темы не просил о прогрессиях, важно чтобы каждый следующий тык левым зубцом был достаточно далеко от предыдущего тыка правой. Т.е. вот эти последовательности не обязаны быть прогрессиями, а только чтоб каждый их член отличался от соответствующего члена прогрессии на неотрицательную монотонно неубывающую величину. Это, кажется, даёт ещё сколько-то свободы в поиске оптимальной тыкательной стратегии

[anahronizm]

waxtep в сообщении #1716528 писал(а):

отдельный вопрос, видимо: является ли такая наивная стратегия оптимальной

Я пробовал разрисовывать отдельные полоски, на каждой из которых проход только одной вилки. Потом накладывал несколько полосок "друг на друга": укладывал одну над другой и смотрел вертикальные результаты. Получалось, что "бить вилкой" в первую свободную ячейку не самый оптимальный путь. Но как найти оптимальный порядок вилок я, конечно, представить не смог.

[wrest]

anahronizm в сообщении #1716568 писал(а):

Получалось, что "бить вилкой" в первую свободную ячейку не самый оптимальный путь.

Тут хотелось бы увидеть пример, чтобы понять критерий "оптимальности". У нас же: либо данная полоска полностью в дырках, либо нет. Если одним способом осталась одна целая клетка, а другим - три, это не говорит нам какой способ лучше, они оба плохие.

[anahronizm]

wrest в сообщении #1716574 писал(а):

хотелось бы увидеть пример

Увы, примера не будет. Просто не помню уже, какие это были "вилки", с какими проходами и какой длины полоску я брал. Просто развлекался, перекладывая в разных положениях, вот и заметил такой момент. Так что строгого утверждения нет.

[waxtep]

wrest в сообщении #1716574 писал(а):

Тут хотелось бы увидеть пример, чтобы понять критерий "оптимальности".

Предлагаю пытаться максимизировать длину полностью покрытой полоски $M(k)$ для данного количества вилок $k$, ну, начиная, конечно, с маленьких $k$, до десятки там например. Не знаю, когда сам до реализации этого предложения доберусь, в выходные наверное.

anahronizm в сообщении #1716568 писал(а):

Получалось, что "бить вилкой" в первую свободную ячейку не самый оптимальный путь

Верю, ведь без труда не выловишь и рыбки из пруда Спасибо за увлекательную задачку

[anahronizm]

waxtep в сообщении #1716580 писал(а):

Спасибо за увлекательную задачку

Рад, что смог дать повод для развлечения.
Если ещё что-то придумаю, напишу.

[waxtep]

waxtep в сообщении #1716555 писал(а):

Т.е. вот эти последовательности не обязаны быть прогрессиями, а только чтоб каждый их член отличался от соответствующего члена прогрессии на неотрицательную монотонно неубывающую величину. Это, кажется, даёт ещё сколько-то свободы в поиске оптимальной тыкательной стратегии

Если действовать не наивно, и забить на прогрессии, точно можно улучшить результат. Посмотрим на примере двух вилок.
I. Наивная стратегия:
- вилка 1, проход 1: (1,3), (6,8), (11,13), ...
- вилка 1, проход 2: (2,4), (9,11), ...
- вилка 2, проход 1: (5,9), ...
- вилка 2, проход 2: (7,11), ...

Мы покрыли 9 клеток подряд, но не 10-ую.

II. Коварно-беспринципная стратегия:
- вилка 1, проход 1: (1,3), (6,8), (11,13), ...
- вилка 1, проход 2: (2,4), ! (10,12), ...
- вилка 2, проход 1: (5,9), ...
- вилка 2, проход 2: (7,11), ...

За счет вольного расположения второго тыка первой вилки во втором проходе мы покрыли уже 13 клеток подряд, но не 14-ую.

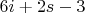
Физически я таскаю в экселе группы клеток, где (вилка $i$, проход $s$) отображается полоской в $6i+2s-3$ клеток, из которых покрашены две клетки, находящиеся на расстоянии $i$ от центральной. Полоски одного вида (размера) не могут налегать друг на друга

-- 29.01.2026, 02:59 --

Тремя вилками могу покрыть $43$ клетки подряд в беспринципной стратегии, в сравнении с $13$ в наивной. В целом, стратегия тоже прямолинейная (и тоже не факт, что оптимальная!): пытаться заткнуть очередную дырку полоской наименьшего размера, не всегда придерживаясь максимально плотного расположения полосок одного размера. Её кстати вроде тоже легко запрогать.
Так, пока рука бойцов колоть устала, перерыв