Математическая статистика (вопрос об определении)

[Hazlarorn]

Товарищи добрый вечер. Возник вопрос по поводу определения при изучении курса (рисунок будет ниже).



Вопрос состоит в том какова область определения оценок в последовательности оценок (извиняюсь за тафтологию)?. И как я понимаю соответсвующая вероятностная мера (в определении) будет определена на сигма алгебре пространства всех возможных последовательностей вещественных чисел (R_infinity). Просто для понимания происходящего в нескольких источниках определение оценки толкуют по разному с одной стороны она своей областью определения имеет соответсвующее пространство элементарных исходов (например где определена выборка конечная), а с другой стороны своей областью определения она имеет множество значений выборки (соответсвующего случайного вектора множество значений). Хотелось бы этот момент как то разъяснить также. Возможно конечно я просто сильно заморачиваюсь по поводу определния.

Возможно для лучшего понимая вопроса я изложу свою версию понимания (возможно она не совсем корректна). Если мы примем первое определение статистики (когда область определения является множеством элементарных исходов где определена исходная выборка) то мне кажется выше данное определение (на скрине не имеет смысла), ибо распределение (от элемента выборки) определена вообще на другом множестве (борелевской сигма алгебре вещественное прямой). Если мы примем второе определение (когда область определения это множество значений[или скорей всего все возможные последовательности вещественных чисел] ,и продолжим вероятностную меру на R_infinity) то тут у меня возникает вопрос практического вычисления таких оценок ибо есть следующий ниже пример для состоятельной оценки.

И да в этом примере тупо применяется ЗБЧ НО вероятностная мера будет на пространстве случайных событий которой соответсвует пространство элементарных исходов где определена вся ВЫБОРКА данная следовательно тут будет применимо первое определение статистики. Возможно конечно что используя определение распределения случайной величины можно показать что это действительно так и есть (т.е. расписать по определению) но мне кажется это слишком сложным для одного определения.




Заранее спасибо

[Ende]

Тема перемещена из форума «Математика (общие вопросы)» в форум «Помогите решить / разобраться (М)»
Причина переноса: вопрос покрывается учебным курсом математической статистики.

[mihaild]

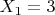
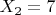
Последовательность оценок определена на последовательностях вещественных чисел. Если я Вам принесу последовательность значений: $X_1 = 3$, $X_2 = 7$, $X_3 = -5$ и т.д., то Вы сможете посчитать каждую из оценок.
Композиция каждой конкретной оценки с соответствующим вектором - это уже случайная величина, определенная на каком-то вероятностном пространстве. На каком - неважно, достаточно, чтобы на нем можно было задать $n$ независимых величин с нужным распределением.
Но да, оценкой часто называют и функцию от значений случайных величин, и композицию (которая сама случайная величина).

Тут нужно заметить, что в определении состоятельности у вас вообще не требуется никакое вероятностное пространство, поддерживающее одновременно все случайные величины. Достаточно для каждого $n$ брать свое пространство, поддерживающее только $n$ величин. Мы сначала для каждого $n$ считаем вероятность, получаем число, а уже потом берем предел по $n$.

[Hazlarorn]

Т.е. на $R_\infty$ (множество всех последовательностей вещественных чисел) для каждого n является областью определения оценки (в последовательности оценок). Правильно ли я понимаю? И еще если так то почему об этом нигде подробно не написано (в различных источниках по крайней мере я про информацию такую не смог найти)

[Ende]

Hazlarorn
Для оформления формул в $\TeX$ ставьте слева и справа от формулы знак доллара. Знак бесконечности кодируется оператором \infty

$R_\infty$

Результат: $R_\infty$

[mihaild]

Hazlarorn в сообщении #1715398 писал(а):

Т.е. на $R_\infty$ (множество всех последовательностей вещественных чисел) для каждого n является областью определения оценки (в последовательности оценок).

Что "является областью определения оценки"?
$n$-я оценка $\hat \theta_n$ в последовательности определена на $\mathbb R^n$. Всю последовательность $\hat \theta$, соответственно, можно определить на $\mathbb R_\infty$ по правилу $\hat\theta(x_1, x_2, \ldots) = (\hat\theta_1(x_1), \hat\theta_2(x_1, x_2), \ldots)$.

[Hazlarorn]

Спасибо. А насчет примера ниже?

[Combat Zone]

Есть два способа смотреть и на выборку, и на статистики, например, то же выборочное среднее. Как на функцию независимых с.в. с распределением $P_\theta$. И как на реализацию этой функции (т.е. когда подставляли конкретные значения, которые $X_1,\ldots X_n$ принимали в результате эксперимента.)

Для того, чтобы говорить о состоятельности или ее отсутствии, необходимо смотреть на статистику (и на выборку) в первом смысле. Тогда при каждом $n$ /оценка $\hat \theta_n = \hat\theta (X_1,\ldots, X_n) = \hat\theta (X_1(\omega),\ldots, X_n(\omega))=\hat\theta_n(\omega)$ - функция, заданная на пространстве элементарных исходов $\Omega$, то есть случайная величина. Омега и есть область определения, если угодно, и на этом не акцентируют внимание, потому что большой нужды в этом акценте нет.

Hazlarorn в сообщении #1715403 писал(а):

А насчет примера ниже?

А что вы хотите знать об этом примере? Уточните вопрос.
И пожалуйста, набирайте, а не скриньте.

[Hazlarorn]

Т.е. в случае асимптотических вопросов. Статистики определяются на пространстве элементарных исходов? Если так то вопросов к примеру данному нет. Но правда в случае если оценка(последовательность оценок) задана на пространстве элементарных исходов то каков смысл Распределения (которое соответсвует последовательности случайных величин) (омега маленькие не принадлежат бореллевской сигма алгебре вещественной прямой) получается тогда вместо распределения нужно (в определение) поставить вероятностную меру определенную там где есть омега маленькие?

Я так понимаю возможно просто переход будет осуществляется от вероятностной меры к распределению через замену переменных? (ВОзможно нет)

[Combat Zone]

Hazlarorn в сообщении #1715923 писал(а):

Т.е. в случае асимптотических вопросов. Статистики определяются на пространстве элементарных исходов? Если так то вопросов к примеру данному нет. Но правда в случае если оценка(последовательность оценок) задана на пространстве элементарных исходов то каков смысл Распределения (которое соответсвует последовательности случайных величин) (омега маленькие не принадлежат бореллевской сигма алгебре вещественной прямой) получается тогда вместо распределения нужно (в определение) поставить вероятностную меру определенную там где есть омега маленькие?

Я так понимаю возможно просто переход будет осуществляется от вероятностной меры к распределению через замену переменных? (ВОзможно нет)

Как бы вам сказать. По отдельности я эти слова знаю. Но в таком порядке не понимаю ни слова. Попробуйте спросить иначе. Может быть, более короткий вопрос задать. Может, формулу написать.

Не надо ничего никуда подставлять.

[Hazlarorn]

.

Вот например (случай когда параметр k-мерный вектор из вещественных чисел). В этом случае последовательность оценок (по вашему определению) будет определена на омега (вверху на листике написано то самое соответсвующее вероятностное пространство) так? В этом случае все оценки имеют одну и ту же область определения (омега)?? Какой тогда смысл самого верхнего определения (начало темы) добавлять внизу индекс тета маленькое? (если мера на F).

Статистика (1 определение): $T_n:\Omega \to \mathbb R$ случайная величина
Статистика (2 определение): $\tau_n:\mathbb R^n \to \mathbb R$, функция от наблюдений $x_1,\dots,x_n$

Так вот я так понял в асимптотических вопросах используется определение номер 1??

[Combat Zone]

Hazlarorn
Вас же просили набирать. Конспект хороший, конечно, а почерк нет, и зрение у меня тоже.
Продраться невозможно.

Hazlarorn в сообщении #1716279 писал(а):

В этом случае последовательность оценок (по вашему определению) будет определена на омега

Hazlarorn в сообщении #1716279 писал(а):

В этом случае все оценки имеют одну и ту же область определения (омега)??

И по вашему, там синим по клетчатому написано.

Hazlarorn в сообщении #1716279 писал(а):

Какой тогда смысл самого верхнего определения (начало темы) добавлять внизу индекс тета маленькое? (если мера на F).

Потому что не зная распределения, вы не посчитаете ни одну из вероятностей, которая нужна для определения (сильной) состоятельности. А распределение задается именно мерой $P_\theta$.

Оставьте скрин, наберите минимальную основу для разговора. Все когда-то не умели набирать.

[Ende]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

наберите необходимые формулы в $\TeX$ (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы)

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Ende]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»
Причина переноса: не указана.

[Hazlarorn]

Вроде исправил вверху написана база для разговора.