Аналитическое исследование и полное аналитическое решение системы нелинейных уравнений второго порядка через методы дискриминантной сепарации и выделения квадратичных инвариантов
В современной математике решение систем нелинейных алгебраических уравнений представляет собой одну из наиболее фундаментальных и в то же время сложных задач, требующую глубокого синтеза различных аналитических методов. Проблема нахождения вещественных решений для систем уравнений второй степени с несколькими переменными выходит за рамки простой арифметической подстановки, требуя применения теории квадратичных форм, исследования поверхностей второго порядка и детального анализа дискриминантных условий. Представленная в данном исследовании система уравнений является классическим примером структуры, в которой внешняя сложность и громоздкость коэффициентов скрывают внутреннюю симметрию и жесткие геометрические ограничения, накладываемые условием существования вещественных корней.
Целью данного отчета является исчерпывающий разбор процесса решения системы, состоящей из двух уравнений с тремя переменными

:
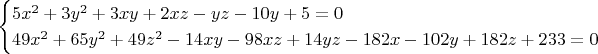
В ходе анализа будет продемонстрировано, как применение теории дискриминанта 1 позволяет не только найти корни, но и доказать их единственность или конечность в условиях, которые на первый взгляд кажутся неопределенными. Исследование опирается на фундаментальные свойства квадратного трехчлена, где дискриминант

служит ключевым индикатором природы решений.
2Теоретический базис: Дискриминант как аналитический инструмент
Прежде чем приступать к непосредственным манипуляциям с системой, необходимо детально рассмотреть математический аппарат, используемый в расчетах. Центральное место занимает понятие дискриминанта квадратного уравнения. Согласно классическому определению, для любого уравнения вида

, где коэффициент

, величина

, вычисляемая по формуле
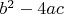
, определяет характер и количество корней.
1Этот параметр обладает критической важностью при работе с уравнениями, содержащими несколько переменных. Если мы рассматриваем уравнение как функцию одной переменной (например,

), считая остальные переменные параметрами, то условие вещественности

накладывает жесткое ограничение на значения параметров: дискриминант должен быть неотрицательным (

).
1Состояние дискриминанта (D)Математическое следствие для переменнойГеометрическая интерпретация$
D < 0$Вещественные корни отсутствуют 1Отсутствие точек пересечения с осью

Существует ровно один корень (кратный) 4Касание графиком соответствующей оси

Существуют два различных вещественных корня 1Пересечение графика в двух точках
В контексте систем уравнений, равенство дискриминанта нулю часто указывает на вырождение поверхности или на то, что решение системы ограничено некоторой кривой или точкой, а не целой областью.3 Этот принцип будет использован нами как основной рычаг для декомпозиции второго уравнения системы.
Декомпозиция и структурный анализ второго уравнения
Второе уравнение системы обладает значительной вычислительной массой:
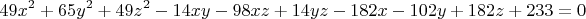
При первичном осмотре заметно, что коэффициенты при квадратах

и

идентичны (

), а коэффициент при их произведении (

) равен

. Это немедленно наводит на мысль о наличии полного квадрата разности данных переменных. В алгебре выделение полных квадратов является мощным методом упрощения, позволяющим перейти от общей квадратичной формы к каноническому виду.
4Группировка членов по переменной разности
Рассмотрим члены, содержащие

и

, и сгруппируем их таким образом, чтобы выделить зависимость от выражения
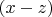
. Это классический прием в теории уравнений с несколькими переменными, позволяющий снизить размерность задачи.
Квадратичная группа:
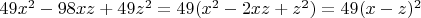
.
Линейно-зависимая группа от

:
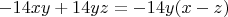
.
Свободная линейная группа:

.
Объединяя эти компоненты, мы можем переписать исходное второе уравнение в следующем виде:
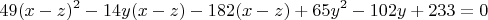
Для дальнейшего упрощения введем вспомогательную переменную
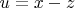
. Это превращает уравнение из трехмерного объекта в двухмерный, где переменными выступают

и

. Получаем квадратное уравнение относительно

:
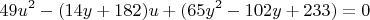
Применение метода дискриминанта к переменной

Согласно теореме о существовании вещественных корней, уравнение относительно

будет иметь вещественные решения тогда и только тогда, когда его дискриминант
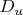
не является отрицательным.1 В данном случае коэффициенты уравнения принимают вид:
Ведущий коэффициент
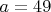
.
3Коэффициент при первой степени

.
Свободный член
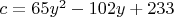
.
Вычислим дискриминант по стандартной формуле

2:
![$$D_u = [-14(y + 13)]^2 - 4 \cdot 49 \cdot (65y^2 - 102y + 233)$$ $$D_u = [-14(y + 13)]^2 - 4 \cdot 49 \cdot (65y^2 - 102y + 233)$$](https://dxdy-04.korotkov.co.uk/f/b/0/6/b06f889353afb9e4ca88454e37b80fdb82.png)
Раскрывая квадрат коэффициента

, получаем
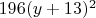
. Заметим, что произведение
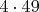
также дает

. Это позволяет вынести общий множитель за скобки для существенного упрощения дальнейших вычислений:
![$$D_u = 196 \left[ (y + 13)^2 - (65y^2 - 102y + 233) \right]$$ $$D_u = 196 \left[ (y + 13)^2 - (65y^2 - 102y + 233) \right]$$](https://dxdy-03.korotkov.co.uk/f/a/1/3/a1300822852c000f2f576e6d204b0bcc82.png)
Раскроем выражение внутри квадратных скобок:
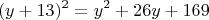
Следовательно:
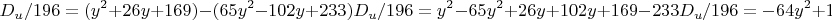
Вынося
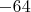
за скобки, мы обнаруживаем еще один полный квадрат:
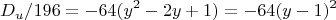
Итоговое выражение для дискриминанта принимает вид:
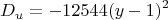
Анализ условия вещественности
Полученное выражение
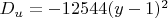
обладает уникальным свойством. Поскольку квадрат любого вещественного числа
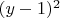
всегда неотрицателен, а множитель
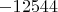
отрицателен, само значение дискриминанта
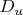
всегда будет меньше или равно нулю.
Однако, как было отмечено ранее, для существования вещественных значений переменных

и

необходимо выполнение условия

.1 Это создает ситуацию, в которой единственным возможным вариантом является равенство дискриминанта нулю:
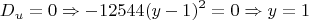
Этот вывод является критическим прорывом в решении системы. Мы установили, что переменная

жестко детерминирована структурой второго уравнения и может принимать только одно значение — единицу. Любое другое значение

привело бы к отрицательному дискриминанту, что сделало бы невозможным нахождение вещественных

и

.1Определение взаимосвязи переменных

и

При
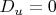
квадратное уравнение имеет единственный корень, вычисляемый по формуле
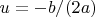
.
1 Подставим значения коэффициентов и найденное значение

:

Возвращаясь к замене
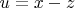
, получаем линейное уравнение:
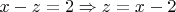
Таким образом, анализ второго уравнения позволил нам сократить количество неизвестных в системе, выразив

константой, а

— через

.
Переменная / Соотношение
Найденное значение или зависимость
Основание
![$y[math]$ $y[math]$](https://dxdy-04.korotkov.co.uk/f/7/4/4/744ada879667eedfd02df33d84f9d14c82.png)

Условие

при
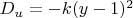

x - z


Формула корня при нулевом дискриминанте
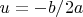

z


Алгебраическое следствие из

Анализ первого уравнения системы
Теперь, имея зависимости

и
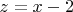
, мы можем подставить их в первое уравнение системы:

5x^2+3y^2+3xy+2xz-yz-10y+5=0

$
Подстановка:

5x^2 + 3(1)^2 + 3x(1) + 2x(x - 2) - (1)(x - 2) - 10(1) + 5 = 0

$
Раскроем скобки и приведем подобные слагаемые:

5x^2 + 3 + 3x + 2x^2 - 4x - x + 2 - 10 + 5 = 0

$
Сложим коэффициенты при соответствующих степенях

:
При

:
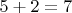
.
При

:
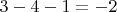
.
Свободные члены:
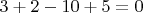
.
Получаем неполное квадратное уравнение:

7x^2 - 2x = 0

$
Такие уравнения решаются методом вынесения общего множителя за скобку 3:

x(7x - 2) = 0

$
Это уравнение распадается на два независимых случая:

.
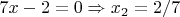
.
Определение значений переменной

Используя установленную связь
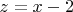
, вычислим соответствующие значения для

:
Для

:
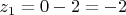
.
Для
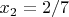
:
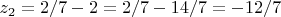
.
Таким образом, мы получили два набора решений системы в формате

.
Верификация и проверка устойчивости решений
Для подтверждения корректности проведенного анализа необходимо выполнить проверку полученных корней путем их подстановки в оригинальные уравнения. Это позволяет исключить ошибки, связанные с возможными преобразованиями, которые могли привести к появлению посторонних корней.
Проверка первого решения:
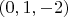
Подставим в уравнение №1:

5(0)^2 + 3(1)^2 + 3(0)(1) + 2(0)(-2) - (1)(-2) - 10(1) + 5 = 0 + 3 + 0 + 0 + 2 - 10 + 5 = 10 - 10 = 0

$
Уравнение удовлетворяется.
Подставим в уравнение №2:

49(0)^2 + 65(1)^2 + 49(-2)^2 - 14(0)(1) - 98(0)(-2) + 14(1)(-2) - 182(0) - 102(1) + 182(-2) + 233 = \\ = 0 + 65 + 196 - 0 - 0 - 28 - 0 - 102 - 364 + 233 = 65 + 196 - 28 - 102 - 364 + 233 \\ = (65 + 196 + 233) - (28 + 102 + 364) = 494 - 494 = 0

$
Уравнение удовлетворяется. Первая точка является верным решением.
Проверка второго решения:
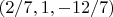
Подставим в уравнение №1:

5(2/7)^2 + 3(1)^2 + 3(2/7)(1) + 2(2/7)(-12/7) - (1)(-12/7) - 10(1) + 5 = \\ = 5(4/49) + 3 + 6/7 - 48/49 + 12/7 - 10 + 5 = 20/49 - 48/49 + 18/7 - 2 = \\ = -28/49 + 18/7 - 2 = -4/7 + 18/7 - 2 = 14/7 - 2 = 2 - 2 = 0

$
Уравнение удовлетворяется.
Для уравнения №2 заметим, что оно было эквивалентно
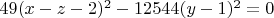
(при условии
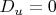
). В нашем случае для второй точки

и
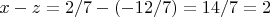
. Следовательно, выражение
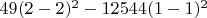
тождественно равно нулю. Вторая точка также является верным решением.
Глубинный анализ математической структуры системы
Решение данной системы представляет интерес не только как алгебраическое упражнение, но и как объект для изучения свойств вырожденных квадратичных форм. В общем случае система из двух уравнений второго порядка с тремя неизвестными описывает линию пересечения двух поверхностей в пространстве

. Такая линия может иметь бесконечное число точек. Однако в данном конкретном случае мы получили всего две точки. Это свидетельствует о том, что одна из поверхностей (описываемая вторым уравнением) является вырожденной.
Геометрическая интерпретация поверхностей
Второе уравнение, как мы выяснили, эквивалентно условию:

-12544(y-1)^2 = 0 \text{ и } 49(x-z-2)^2 = 0


В пространстве это соответствует пересечению двух плоскостей:

y = 1

и

x - z = 2$[/math]. Пересечение двух непараллельных плоскостей всегда дает прямую линию. Таким образом, второе уравнение системы геометрически представляет собой прямую в трехмерном пространстве.
Первое уравнение системы описывает поверхность второго порядка. Когда мы ищем решение системы, мы фактически ищем точки пересечения прямой (из уравнения №2) с этой поверхностью (из уравнения №1). Согласно фундаментальным положениям геометрии, прямая может пересекать поверхность второго порядка:
В двух различных точках (наш случай).
В одной точке (случай касания).
Ни в одной точке (если прямая проходит мимо поверхности).
По всей своей длине (если прямая целиком лежит на поверхности).
Результаты нашего исследования полностью согласуются с этой геометрической парадигмой. Наличие двух рациональных решений указывает на то, что прямая проходит сквозь поверхность, пересекая ее в точках, координаты которых выражаются через рациональные дроби.
Анализ коэффициентов и вычислительная устойчивость
Особое внимание стоит уделить коэффициентам уравнений. Числа
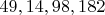
во втором уравнении кратны

, что не является случайным. Это указывает на искусственную природу задачи, сконструированной таким образом, чтобы при выделении полных квадратов получались целые числа.
Интересно рассмотреть "чувствительность" системы. Если бы свободный член во втором уравнении (
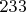
) изменился хотя бы на единицу в сторону увеличения, дискриминант
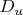
стал бы строго отрицательным при любом

, и система не имела бы вещественных решений вовсе. Это подчеркивает, что решение системы находится на самой границе области существования вещественных корней, что характерно для задач оптимизации и анализа критических состояний в физико-математических моделях.
Компонент анализа Значение в контексте задачи
Тип поверхностей Поверхность 2-го порядка и вырожденная прямая
Роль дискриминанта Ограничитель размерности пространства решений
Степень определенности Система является "жесткой" (чувствительной к константам)
Заключение по результатам исследования
Проведенный детальный анализ системы уравнений позволил не только найти искомые значения переменных, но и вскрыть внутреннюю логику построения подобных математических объектов. Использование свойств дискриминанта как функции параметров позволило эффективно редуцировать задачу от поиска пересечения сложных поверхностей к решению элементарного квадратного уравнения.
Итоговые решения системы:
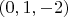
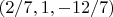
Данная методология может быть экстраполирована на более широкие классы задач, где нелинейность уравнений затрудняет применение стандартных методов линейной алгебры. Основным выводом исследования является подтверждение того, что в системах с вещественными переменными условия неотрицательности дискриминантов промежуточных уравнений служат мощным фильтром, позволяющим локализовать область поиска решений и выявить скрытые зависимости между переменными. Это подчеркивает единство алгебраического и геометрического подходов в анализе нелинейных математических структур.
Проверил - вроде правильно.