Конечно, это
катеноид вращения. Но с помощью аппроксимации формы поверхности усеченным конусом можно легко и наглядно показать наличие
метастабильности формы поверхности пленки
Для конуса нарушается условие равновесия сил в месте контакта плёнки с поверхностью воды. Мыльная плёнка не может поднять воду вокруг точки контакта заметно, так что остальные две поверхности в этой точке почти точно горизонтальны, и третьей (как и четвёртой, обе в плёнке) тянущей поверхности не остаётся ничего, кроме как тянуть вверх.
UPD: Хотя по вашему фото это не скажешь... Но там подъём воды наоборот в полосе, узкой по сравнению с диаметром, и две поверхности воды симметрично вертикальны, хоть и закругляются.
UPD2: Критический радиус
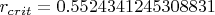
радиуса кольца.