Мыльный пузырь 3(мыльная пленка)

[druggist]

Тонкое пластмассовое кольцо радиуса R находится на поверхности мыльного раствора и смачивается жидкостью. Кольцо плавно подымают над поверхностью на высоту Н так, что плоскость кольца все время горизонтальна. При этом с увеличением Н между жидкостью и кольцом растягивается мыльная пленка, имеющая форму боковой поверхности усеченного конуса (с фиксированным радиусом основания R). При какой высоте пленка оторвется от поверхности мыльного раствора и расположится в плоскости кольца?(Форма поверхности, скорее всего не просто конусная, но в эксперименте была очень близка к данной)

[realeugene]

druggist в сообщении #1712410 писал(а):

При этом с увеличением Н между жидкостью и кольцом растягивается мыльная пленка, имеющая форму боковой поверхности усеченного конуса (с фиксированным радиусом основания R).

У меня не получается представить себе эту ситуацию. Рисунок был бы полезен.

[amon]

druggist в сообщении #1712410 писал(а):

При этом с увеличением Н между жидкостью и кольцом растягивается мыльная пленка, имеющая форму боковой поверхности усеченного конуса (с фиксированным радиусом основания R).

С чего вдруг? Пленка стремится максимально сократить свою поверхность, и без дополнительных ухищрений ничего, кроме плоской пленки, натянутой на кольцо, Вы так не получите.

[realeugene]

Надо просто найти argmin боковой поверхности усечённого конуса по радиуса малого основания при заданных радиусе большого основания и высоте, и посмотреть, при какой высоте он станет нулём?

[amon]

amon в сообщении #1712417 писал(а):

ничего, кроме плоской пленки, натянутой на кольцо, Вы так не получите.

Глупость написал. Конуса не будет. Насколько то, что получится отличается от конуса сходу не соображу.

[realeugene]

amon в сообщении #1712426 писал(а):

Конуса не будет. Насколько то, что получится отличается от конуса сходу не соображу.

Если я не ошибся в выкладках, форма поверхности подчиняется уравнению

$$r''=\frac{1+{\left(r'\right)}^2}r$$

Вообще из нулевой разности давлений понятно, что суммарная кривизна поверхности всюду равна нулю. Так что наверное можно эту формулу записать и прямо, но как с ходу не соображу, и пока нет времени продолжать.

[Geen]

realeugene в сообщении #1712431 писал(а):

кривизна поверхности

Вообще говоря, у плёнки две поверхности...

[realeugene]

Geen в сообщении #1712432 писал(а):

Вообще говоря, у плёнки две поверхности...

И обе одинаково натянутые, так что пофиг что их две.

[druggist]

realeugene в сообщении #1712422 писал(а):

Надо просто найти argmin боковой поверхности усечённого конуса по радиуса малого основания при заданных радиусе большого основания и высоте, и посмотреть, при какой высоте он станет нулём?

Да, именно так я и рассуждал:

$$S_b = \pi (R+r) \sqrt{(H^2 + (R-r)^2)}$$

При малых $H<<R$ имеем минимум $S_b$ при $r\approx R$ и в т. $r=0$ - максимум. Далее ситуация похожа на фазовый переход первого рода - при увеличении H имеем два минимума $r=0$ и $r= R_m<R$ между которыми максимум - потенциальный барьер.

[Geen]

realeugene
Но тогда, и конус сойдёт....

[realeugene]

Geen в сообщении #1712438 писал(а):

Но тогда, и конус сойдёт....

Нет.

Проще мыслить через энергию. Форма поверхности будет такая, чтобы функционал энергии был минимальным при заданных граничных условиях. Поверхностная энергия пропорциональна площади поверхности. Плёнка тонкая - две поверхности одинаковой формы вместо одной просто удваивают поверхностную энергию.

Соответственно, две поверхности вместо одной просто удваивают разность давлений, давая одинаковые прибавки давления (и одного знака), пропорциональные их средней кривизне.

Уравнение выше я записал, посчитав поверхность осесимметричной и проварьировав её площадь.

[realeugene]

realeugene в сообщении #1712431 писал(а):

$$r''=\frac{1+{\left(r'\right)}^2}r$$

Хм... Полуокружность удовлетворяет уравнению с точностью до знака.

UPD: Правильно: мыльный пузырь - это не решение данного уравнения: в нём давление внутри больше, чем снаружи.

[amon]

Скетч "точного" решения. Со времен Эйлера известно точное решение для пленки, натянутой между двумя одинаковыми параллельными кольцами, расположенными на расстоянии $L.$ Для сокращения числа букв радиус колец будем считать единицей длины ($R=1$). Тогда поверхность пленки - поверхность, образованная вращением цепной линии
$y=r\ch\frac{x}{r}$
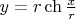
вокруг оси $X.$
$r$ - радиус перетяжки, который определяется из уравнения
$\ch\frac{L}{2r}=\frac{1}{r}. $
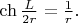
(Линия должна проходить через точку $y=1$ при $x=L/2$.)
Пленка между поверхностью раствора и кольцом должна быть "половиной" такой поверхности (поверхностью для $x>0$), а кольцо на поверхности - кольцом радиуса $r.$ Действительно, если это не так, то отразив эту поверхность получим решение для двух колец, отличное от эйлерового, а таких нет.
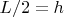
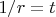
Обозначив $L/2=h$ - высота кольца над поверхностью раствора, и $1/r=t$ получим уравнение на $r(h)$
$\ch( ht)=t.$
Это - пересечение кошинуса с прямой. При некотором достаточно большом $h$ оно решений не имеет. При малых $h$ у него два решения, одно из которых, видимо, неустойчиво. Точка совпадения решений соответствует предельному $h,$ при котором пленка отрывается от поверхности и распрямляется на кольце. Картинки нарисовать не могу - компьютер накрылся, и пока на нем ничего не стоит из рисовалок. Так что, как говорил в подобных случаях Эйлер: "Дальше решай кто может".

[realeugene]

amon в сообщении #1712452 писал(а):

$y=r\ch\frac{x}{r}$

О, только что хотел написать найденное решение уравнения.

[realeugene]

amon в сообщении #1712452 писал(а):

$\ch( ht)=t$

В совпадающих корнях ещё и производные совпадают, откуда $h\cdot\sh(t)=1$, и воспользовавшись тождеством $\ch^2 x - \sh^2 x = 1$ получаем $t = \sqrt{1 + 1/h^2}$.
Уравнение $\ch{\sqrt{1 + h^2}}=\sqrt{1+1/h^2}$ видимо можно решить только численно. Получаем $h_{crit} = 0.6627434193491816$