Если честно, тяжеловато воспринимаю формулы, связывающие эти морфизмы (аксиомы бипроизведения):
Ну так рассмотрите простой пример
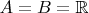
в категории конечномерных векторных пространств над

. Тогда
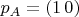
,
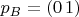
,
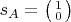
,
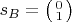
. В частности,
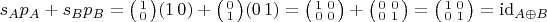
.
Пытаетесь сказать, что компоненты морфизма - своеобразный базис?
Скорее, разложение в прямую сумму, базисов там всё-таки нет. Точнее,
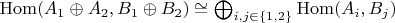
, где в правой части прямая сумма абелевых групп, в левой прямая сумма в категории, и изоморфизм абелевых групп.
Например, есть категория банаховых пространств над

и непрерывных отображений. В ней есть пространство

последовательностей, сходящихся к

, и пространство

из всех сходящихся последовательностей. Есть разложение в прямую сумму
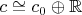
. А естественных базисов в

и

нет.
Вообще стандартный пример абелевых категорий — это категории правых (или левых) модулей над ассоциативным кольцом с единицей. Если с прямой суммой модулей вам всё понятно, то и матричная запись для гомоморфизмов между прямыми суммами должна быть естественной.